【题目】如果![]() 的定义域为
的定义域为![]() ,对于定义域内的任意
,对于定义域内的任意![]() ,存在实数
,存在实数![]() 使得
使得![]() 成立,则称此函数具有“
成立,则称此函数具有“![]() 性质”.给出下列命题:
性质”.给出下列命题:
①函数![]() 具有“
具有“![]() 性质”;
性质”;
②若奇函数![]() 具有“
具有“![]() 性质”,且
性质”,且![]() ,则
,则![]() ;
;
③若函数![]() 具有“
具有“![]() 性质”, 图象关于点
性质”, 图象关于点![]() 成中心对称,且在
成中心对称,且在![]() 上单调递减,则
上单调递减,则![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
④若不恒为零的函数![]() 同时具有“
同时具有“![]() 性质”和 “
性质”和 “![]() 性质”,且函数
性质”,且函数![]() 对
对![]() ,都有
,都有![]() 成立,则函数
成立,则函数![]() 是周期函数.
是周期函数.
其中正确的是 (写出所有正确命题的编号).
参考答案:
【答案】①③④
【解析】
试题分析:由题意得,①![]() ,所以函数
,所以函数![]() 具有“
具有“![]() 性质”,所以是正确的;②因为奇函数
性质”,所以是正确的;②因为奇函数![]() ,具有“
,具有“![]() 性质”,所以
性质”,所以![]() ,所以
,所以![]() ,周期为
,周期为![]() ,因为
,因为![]() ,所以不正确;③因为函数
,所以不正确;③因为函数![]() 具有“
具有“![]() 性质”,所以
性质”,所以![]() ,所以
,所以![]() 关于
关于![]() 对称,即
对称,即![]() ,因为图象关于点
,因为图象关于点![]() 对称,所以
对称,所以![]() ,即
,即![]() ,所以函数
,所以函数![]() 为偶函数,因为图象关于点
为偶函数,因为图象关于点![]() 成中心对称,且在
成中心对称,且在![]() 上单调递减,所以图象也关于点
上单调递减,所以图象也关于点![]() 成中心对称,且在
成中心对称,且在![]() 上单调递减,根据偶函数的对称得出,在
上单调递减,根据偶函数的对称得出,在![]() 上单调递增,所以是正确的;④因为“
上单调递增,所以是正确的;④因为“![]() 性质”和“
性质”和“![]() 性质”,所以
性质”,所以![]() ,
,
所以![]() 为偶函数,且周期为
为偶函数,且周期为![]() ,因为函数
,因为函数![]() ,对
,对![]() ,都有
,都有![]() 成立,所以
成立,所以![]() 必是周期函数,所以是正确的,故选①③④.
必是周期函数,所以是正确的,故选①③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知圆
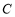 的极坐标方程为
的极坐标方程为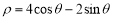 ,直线
,直线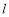 的参数方程为
的参数方程为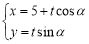 (
(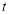 为参数).若直线
为参数).若直线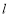 与圆
与圆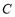 相交于不同的两点
相交于不同的两点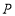 ,
,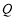 .
.(Ⅰ)写出圆
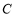 的直角坐标方程,并求圆心的坐标与半径;
的直角坐标方程,并求圆心的坐标与半径;(Ⅱ)若弦长
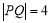 ,求直线
,求直线 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
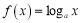 ,
,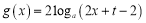 ,其中
,其中 且
且 ,
,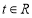 .
.(1)若
 ,且
,且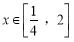 时,
时,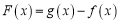 的最小值是
的最小值是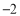 ,求实数
,求实数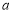 的值;
的值;(2)若
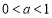 ,且
,且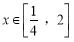 时,有
时,有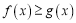 恒成立,求实数
恒成立,求实数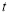 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
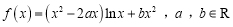 .
.(Ⅰ)当
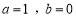 时,求曲线
时,求曲线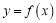 在点
在点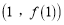 处的切线方程;
处的切线方程;(Ⅱ)当
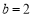 时,若对任意
时,若对任意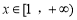 ,不等式
,不等式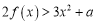 恒成立,求实数
恒成立,求实数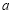 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于命题:三角形的内角至多有一个是钝角,若用反证法证明,正确的反设是 ________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正三棱柱
 中,点
中,点 是棱
是棱 的中点,
的中点, .
.
(1)求证:
 平面
平面 ;
;(2)求二面角
 的平面角的正弦值.
的平面角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】流程图中的判断框有1个入口和________个出口.
相关试题

