【题目】对于命题:三角形的内角至多有一个是钝角,若用反证法证明,正确的反设是 ________
参考答案:
【答案】假设至少有两个钝角
【解析】分析:求出要证命题:“三角形的内角至多有一个钝角”的否定为“三角形的内角至少有两个钝角”,从而得到结论.
详解:用反证法证明数学命题时,应先假设要证的命题的否定成立,
而要证命题:“三角形的内角至多有一个钝角”的否定为“三角形的内角至少有两个钝角”,故应先假设三角形的内角至少有两个钝角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
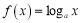 ,
,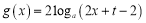 ,其中
,其中 且
且 ,
,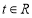 .
.(1)若
 ,且
,且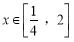 时,
时,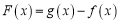 的最小值是
的最小值是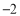 ,求实数
,求实数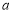 的值;
的值;(2)若
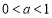 ,且
,且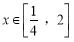 时,有
时,有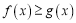 恒成立,求实数
恒成立,求实数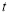 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
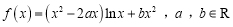 .
.(Ⅰ)当
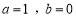 时,求曲线
时,求曲线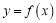 在点
在点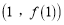 处的切线方程;
处的切线方程;(Ⅱ)当
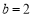 时,若对任意
时,若对任意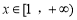 ,不等式
,不等式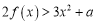 恒成立,求实数
恒成立,求实数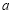 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果
 的定义域为
的定义域为 ,对于定义域内的任意
,对于定义域内的任意 ,存在实数
,存在实数 使得
使得 成立,则称此函数具有“
成立,则称此函数具有“ 性质”.给出下列命题:
性质”.给出下列命题:①函数
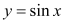 具有“
具有“ 性质”;
性质”;②若奇函数
 具有“
具有“ 性质”,且
性质”,且 ,则
,则 ;
;③若函数
 具有“
具有“ 性质”, 图象关于点
性质”, 图象关于点 成中心对称,且在
成中心对称,且在 上单调递减,则
上单调递减,则 在
在 上单调递减,在
上单调递减,在 上单调递增;
上单调递增;④若不恒为零的函数
 同时具有“
同时具有“ 性质”和 “
性质”和 “ 性质”,且函数
性质”,且函数 对
对 ,都有
,都有 成立,则函数
成立,则函数 是周期函数.
是周期函数.其中正确的是 (写出所有正确命题的编号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正三棱柱
 中,点
中,点 是棱
是棱 的中点,
的中点, .
.
(1)求证:
 平面
平面 ;
;(2)求二面角
 的平面角的正弦值.
的平面角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】流程图中的判断框有1个入口和________个出口.
-
科目: 来源: 题型:
查看答案和解析>>【题目】重庆一中开展的“第十届校园田径运动会”中,甲、乙、丙、丁四位同学每人参加了一个项目,且参加的项目各不相同,这个四个项目分别是:跳高、跳远、铅球、跑步.下面是关于他们各自参加的活动的一些判断:
①甲不参加跳高,也不参加跳远;②乙不参加跳远,也不参加铅球;
③丙不参加跳高,也不参加跳远;④如果甲不参加跑步,则丁也不参加跳远.
已知这些判断都是正确的,则乙参加了__________.
相关试题

