【题目】如图所示，某游乐园的一个摩天轮半径为10米，轮子的底部在地面上2米处，如果此摩天轮每20分钟转一圈，当摩天轮上某人经过
处时开始计时（按逆时针方向转），
（其中
平行于地面）.
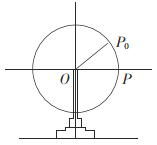
（1）求开始转动5分钟时此人相对于地面的高度.
（2）开始转动
分钟时，摩天轮上此人经过点
，求
的值.
【答案】（1）
（米）；（2）10
【解析】
（1）根据题意以
为坐标原点，以
所在直线为
轴建立平面直角坐标系，可求得在
分钟时此人相对于地面高度的解析式，代入
即可求解.
（2）由题意可知转动
分钟时转过的角度，即可求得
的坐标；根据题意可求得
的坐标，由两点间距离公式即可求得
的值.
（1）以为坐标原点，以所在直线为轴建立平面直角坐标系，如下图所示：
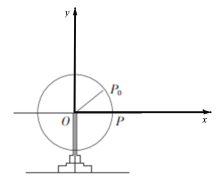
设摩天轮上某人所在的点为
，则在分钟内
转过的角为
，
摩天轮半径为10米，轮子的底部在地面上2米处，
所以分钟时，点的纵坐标为
，
所以在分钟时此人相对于地面的高度为
，
所以5分钟后的高度为
（米）.
（2）由（1）可知，在分钟内转过的角为
，
，
由题意可知
，
由
可求得
，
则由两点间距离公式可得
.
轻巧夺冠周测月考直通中考系列答案科目：高中数学 来源： 题型：
【题目】已知函数f（x）＝（k＋
）lnx＋
，k∈[4，＋∞），曲线y＝f（x）上总存在两点M（x1，y1），N（x2，y2），使曲线y＝f（x）在M，N两点处的切线互相平行，则x1＋x2的取值范围为
A. （
，＋∞） B. （
，＋∞） C. [，＋∞） D. [，＋∞）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
，
.
（1）当
时，若对任意
均有
成立，求实数
的取值范围；
（2）设直线
与曲线
和曲线
相切，切点分别为
，
，其中
.
①求证：
；
②当
时，关于
的不等式
恒成立，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位：kg）, 其频率分布直方图如下：
（1）记A表示事件“旧养殖法的箱产量低于50 kg”，估计A的概率；
（2）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：
箱产量＜50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
（3）根据箱产量的频率分布直方图，对这两种养殖方法的优劣进行比较.
附：
P（ | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了解甲、乙两个快递公司的工作状况，假设同一个公司快递员的工作状况基本相同，现从甲、乙两公司各随机抽取一名快递员，并从两人某月（30天）的快递件数记录结果中随机抽取10天的数据，制表如图：
每名快递员完成一件货物投递可获得的劳务费情况如下：甲公司规定每件4.5元；乙公司规定每天35件以内（含35件）的部分每件4元，超出35件的部分每件7元.
（1）根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数；
（2）为了解乙公司员工B的每天所得劳务费的情况，从这10天中随机抽取1天，他所得的劳务费记为X（单位：元），求X的分布列和数学期望；
（3）根据表中数据估算两公司的每位员工在该月所得的劳务费.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给定椭圆
，称圆心在原点
，半径为
的圆是椭圆
的“准圆”.若椭圆
的一个焦点为
，其短轴上的一个端点到
的距离为
.
（1）求椭圆
的方程和其“准圆”方程；
（2）点
是椭圆
的“准圆”上的动点，过点
作椭圆的切线
交“准圆”于点
.
①当点
为“准圆”与
轴正半轴的交点时，求直线
的方程并证明
；
②求证：线段
的长为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
