【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,若对任意
时,若对任意![]() 均有
均有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(2)设直线![]() 与曲线
与曲线![]() 和曲线
和曲线![]() 相切,切点分别为
相切,切点分别为![]() ,
,![]() ,其中
,其中![]() .
.
①求证:![]() ;
;
②当![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)①证明见解析;②
;(2)①证明见解析;②![]() .
.
【解析】
(1)依据题意得出![]() ,利用导数分别求出函数
,利用导数分别求出函数![]() 和
和![]() 在
在![]() 上的最小值和最大值,进而可求得实数
上的最小值和最大值,进而可求得实数![]() 的取值范围;
的取值范围;
(2)①由题意可得![]() ,可得出
,可得出![]() ,再由
,再由![]() 可得出结论;
可得出结论;
②得到![]() ,设
,设![]() ,利用导数求出函数
,利用导数求出函数![]() 的最大值,从而求出
的最大值,从而求出![]() 的范围即可.
的范围即可.
(1)当![]() 时,
时,![]() ,由
,由![]() ,得
,得![]() ,
,
依题意可得![]() 对任意的
对任意的![]() 恒成立,
恒成立,
设![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以,函数![]() 在
在![]() 处取得极小值,亦即最小值,即
处取得极小值,亦即最小值,即![]() .
.
设![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以,函数![]() 在
在![]() 处取得极大值,亦即最大值,即
处取得极大值,亦即最大值,即![]() .
.
所以,![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() ;
;
(2)由已知![]() ,
,![]() .
.
①![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() .
.
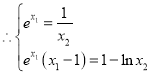 .
.
![]() ,
,![]() ,即
,即![]() ,所以
,所以![]() ;
;
②由①知![]() ,
,![]() 且
且![]() ,
,
由![]() ,得
,得![]() ,
,
设![]() ,
,![]() ,
,
所以,函数![]() 在
在![]() 为减函数,
为减函数,![]() ,
,
由![]() ,
,![]() ,
,
又![]() ,
,![]() .
.

