【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
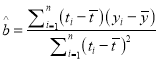 ,
, ![]()
参考答案:
【答案】(1)![]() ;(2)6.8千元.
;(2)6.8千元.
【解析】试题分析:(1)根据所给的数据,利用最小二乘法可得横标和纵标的平均数,横标和纵标的积的和,与横标的平方和,代入公式求出b的值,再求出a的值,写出线性回归方程.
(2)根据上一问做出的线性回归方程,代入所给的t的值,预测该地区2015年农村居民家庭人均纯收入,这是一个估计值.
试题解析:(1)由题意, ![]() ,
,
![]() ,
,
![]() ,
,
![]()
∴y关于t的线性回归方程为![]() ; 8分
; 8分
(2)由(1)知,b=0.5>0,故2007年至2013年该地区农村居民家庭人均纯收入逐年增加,平均每年增加0.5千元.
将2015年的年份代号t=9代入![]() ,得:
,得: ![]() (千元)
(千元)
故预测该地区2015年农村居民家庭人均纯收入为6.8千元左右. 12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a1 , a2 , a3 , …a20这20个数据的平均数为
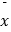 ,方差为0.21,则a1 , a2 , a3 , …a20 ,
,方差为0.21,则a1 , a2 , a3 , …a20 , 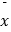 这21个数据的方差为( )
这21个数据的方差为( )
A.0.19
B.0.20
C.0.21
D.0.22 -
科目: 来源: 题型:
查看答案和解析>>【题目】节日前夕,小李在家门前的树上挂了两串彩灯,这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮,那么这两串彩灯同时通电后,它们第一次闪亮的时候相差不超过2秒的概率是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知
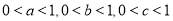 ,用分析法证明:
,用分析法证明: 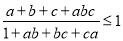 ;
;(2)已知
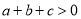 ,
, 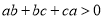 且
且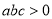 ,用反证法证明:
,用反证法证明: 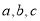 都大于零.
都大于零. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△AOB中,∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,△AOC为钝角三角形的概率是( )
A.0.2
B.0.4
C.0.6
D.0.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}中,a1=
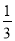 ,前n项和Sn满足Sn+1-Sn=(
,前n项和Sn满足Sn+1-Sn=(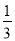 )n+1(n∈N*).
)n+1(n∈N*).(1)求数列{an}的通项公式an以及前n项和Sn;
(2)若S1,t(S1+S2),3(S2+S3)成等差数列,求实数t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】过点
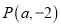 作抛物线
作抛物线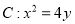 的两条切线, 切点分别为
的两条切线, 切点分别为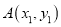 ,
, 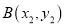 .
.(1) 证明:
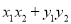 为定值;
为定值;(2) 记△
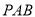 的外接圆的圆心为点
的外接圆的圆心为点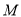 , 点
, 点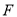 是抛物线
是抛物线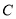 的焦点, 对任意实数
的焦点, 对任意实数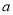 , 试判断以
, 试判断以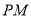 为直径的圆是否恒过点
为直径的圆是否恒过点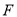 ? 并说明理由.
? 并说明理由.
相关试题

