【题目】已知y=f(x)是定义在R上的奇函数,且 ![]() 为偶函数,对于函数y=f(x)有下列几种描述:①y=f(x)是周期函数②x=π是它的一条对称轴;③(﹣π,0)是它图象的一个对称中心;④当
为偶函数,对于函数y=f(x)有下列几种描述:①y=f(x)是周期函数②x=π是它的一条对称轴;③(﹣π,0)是它图象的一个对称中心;④当 ![]() 时,它一定取最大值;其中描述正确的是 .
时,它一定取最大值;其中描述正确的是 .
参考答案:
【答案】①③
【解析】解:∵ ![]() 为偶函数∴f(﹣x+
为偶函数∴f(﹣x+ ![]() )=f(x+
)=f(x+ ![]() ),对称轴为
),对称轴为 ![]()
而y=f(x)是定义在R上的奇函数
∴f(﹣x+ ![]() )=﹣f(x﹣
)=﹣f(x﹣ ![]() )=f(x+
)=f(x+ ![]() )
)
即f(x+ ![]() )=﹣f(x﹣
)=﹣f(x﹣ ![]() ),f(x+π)=﹣f(x),f(x+2π)=f(x)
),f(x+π)=﹣f(x),f(x+2π)=f(x)
∴y=f(x)是周期函数,故①正确
x= ![]() (k∈Z)是它的对称轴,故②不正确
(k∈Z)是它的对称轴,故②不正确
(﹣π,0)是它图象的一个对称中心,故③正确
当 ![]() 时,它取最大值或最小值,故④不正确
时,它取最大值或最小值,故④不正确
所以答案是:①③
【考点精析】解答此题的关键在于理解函数奇偶性的性质的相关知识,掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列不等式组中,同解的是 ( )
A.
 与
与 B.
B.  与x2﹣3x+2>0
与x2﹣3x+2>0C.
 >0与
>0与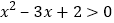 D.
D.  (x﹣2)≥0与
(x﹣2)≥0与
-
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f′(x)﹣g(x)(f′(x)为函数f(x)的导函数)在[a,b]上有且只有两个不同的零点,则称f(x)是g(x)在[a,b]上的“关联函数”.若f(x)=
 +4x是g(x)=2x+m在[0,3]上的“关联函数”,则实数m的取值范围是( )
+4x是g(x)=2x+m在[0,3]上的“关联函数”,则实数m的取值范围是( )
A.
B.[﹣1,0]
C.(﹣∞,﹣2]
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共
 个,生产一个卫兵需
个,生产一个卫兵需 分钟,生产一个骑兵需
分钟,生产一个骑兵需 分钟,生产一个伞兵需
分钟,生产一个伞兵需 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过 小时,若生产一个卫兵可获利润
小时,若生产一个卫兵可获利润 元,生产一个骑兵可获利润
元,生产一个骑兵可获利润 元,生产一个伞兵可获利润
元,生产一个伞兵可获利润 元.
元.(1)用每天生产的卫兵个数
 与骑兵个数
与骑兵个数 表示每天的利润
表示每天的利润 (元);
(元);(2)怎么分配生产任务才能使每天的利润最大,最大利润是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】若对任意x∈A,y∈B,(AR,BR)有唯一确定的f(x,y)与之对应,则称f(x,y)为关于x、y的二元函数.现定义满足下列性质的二元函数f(x,y)为关于实数x、y的广义“距离”;
(1)非负性:f(x,y)≥0,当且仅当x=y时取等号;
(2)对称性:f(x,y)=f(y,x);
(3)三角形不等式:f(x,y)≤f(x,z)+f(z,y)对任意的实数z均成立.
今给出三个二元函数,请选出所有能够成为关于x、y的广义“距离”的序号:
①f(x,y)=|x﹣y|;②f(x,y)=(x﹣y)2;③ .
.
能够成为关于的x、y的广义“距离”的函数的序号是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=ax2+bx+c(a,b,c∈R)满足:对任意实数x,都有f(x)≥x,且当x∈(1,3)时,有f(x)≤
 (x+2)2成立.
(x+2)2成立.(1)证明:f(2)=2;
(2)若f(-2)=0,求f(x)的表达式;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.
(Ⅰ)求f(x)的单调递减区间;
(Ⅱ)设α是锐角,且 ,求f(α)的值.
,求f(α)的值.
相关试题

