【题目】已知函数 ![]() .
.
(Ⅰ)求f(x)的单调递减区间;
(Ⅱ)设α是锐角,且 ![]() ,求f(α)的值.
,求f(α)的值.
参考答案:
【答案】解:(Ⅰ) ![]() =
= ![]() cos2x﹣
cos2x﹣ ![]() sin2x=
sin2x= ![]() cos2x. 由 2kπ≤2x≤2kπ+π,k∈z,可得 kπ≤x≤kπ+
cos2x. 由 2kπ≤2x≤2kπ+π,k∈z,可得 kπ≤x≤kπ+ ![]() ,故求f(x)的单调递减区间为[kπ,kπ+
,故求f(x)的单调递减区间为[kπ,kπ+ ![]() ],k∈z.
],k∈z.
(Ⅱ)∵α是锐角,且 ![]() ,∴
,∴ ![]() =
= ![]() ,α=
,α= ![]() .
.
∴f(α)= ![]() cos2x=
cos2x= ![]() cos
cos ![]() =
= 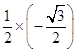 =﹣
=﹣ ![]()
【解析】(Ⅰ) ![]() =
= ![]() cos2x,由 2kπ≤2x≤2kπ+π,k∈z,求得f(x)的单调递减区间.(Ⅱ)由 α是锐角,且
cos2x,由 2kπ≤2x≤2kπ+π,k∈z,求得f(x)的单调递减区间.(Ⅱ)由 α是锐角,且 ![]() ,得
,得 ![]() =
= ![]() ,α=
,α= ![]() ,故 f(α)=
,故 f(α)= ![]() cos2x=
cos2x= ![]() cos
cos ![]() .
.
【考点精析】本题主要考查了两角和与差的正弦公式和正弦函数的单调性的相关知识点,需要掌握两角和与差的正弦公式:![]() ;正弦函数的单调性:在
;正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数才能正确解答此题.
上是减函数才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=f(x)是定义在R上的奇函数,且
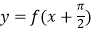 为偶函数,对于函数y=f(x)有下列几种描述:①y=f(x)是周期函数②x=π是它的一条对称轴;③(﹣π,0)是它图象的一个对称中心;④当
为偶函数,对于函数y=f(x)有下列几种描述:①y=f(x)是周期函数②x=π是它的一条对称轴;③(﹣π,0)是它图象的一个对称中心;④当 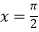 时,它一定取最大值;其中描述正确的是 .
时,它一定取最大值;其中描述正确的是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】若对任意x∈A,y∈B,(AR,BR)有唯一确定的f(x,y)与之对应,则称f(x,y)为关于x、y的二元函数.现定义满足下列性质的二元函数f(x,y)为关于实数x、y的广义“距离”;
(1)非负性:f(x,y)≥0,当且仅当x=y时取等号;
(2)对称性:f(x,y)=f(y,x);
(3)三角形不等式:f(x,y)≤f(x,z)+f(z,y)对任意的实数z均成立.
今给出三个二元函数,请选出所有能够成为关于x、y的广义“距离”的序号:
①f(x,y)=|x﹣y|;②f(x,y)=(x﹣y)2;③ .
.
能够成为关于的x、y的广义“距离”的函数的序号是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=ax2+bx+c(a,b,c∈R)满足:对任意实数x,都有f(x)≥x,且当x∈(1,3)时,有f(x)≤
 (x+2)2成立.
(x+2)2成立.(1)证明:f(2)=2;
(2)若f(-2)=0,求f(x)的表达式;
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,a、b、c分别是角A、B、C的对边,且
 =﹣
=﹣  .
.
(Ⅰ)求角B的大小;
(Ⅱ)若b= ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】数列
 满足递推式
满足递推式
(1)求a1,a2,a3;
(2)若存在一个实数
 ,使得
,使得 为等差数列,求
为等差数列,求 值;
值;(3)求数列{
 }的前n项之和.
}的前n项之和. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱
 中,
中, 是
是 上的一点,
上的一点, ,且
,且 .
.
(1)求证:
 平面
平面 ;
;(2)若
 ,求点
,求点 到平面
到平面 的距离.
的距离.
相关试题

