【题目】写出下列命题的否定,并判断其真假:
(1)p:不论m取何实数,方程x2+x-m=0必有实数根;
(2)q:存在一个实数x,使得x2+x+1≤0;
(3)r:等圆的面积相等,周长相等.
参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】试题分析:(1)先判断命题为全称命题,那么否定为特称命题,由判别式判断跟的个数即可知命题真假;
(2)先判断知函数为特称命题,那么否定为全称命题,利用配方可知命题真假;
(3)先判断命题为全称命题,那么否定为特称命题,由圆的面积和周长公式可得真假.
试题解析:
(1)这一命题可以表述为p:“对所有的实数m,方程x2+x-m=0有实数根”,
其否定形式是![]() p:“存在实数m,使得x2+x-m=0没有实数根”.
p:“存在实数m,使得x2+x-m=0没有实数根”.
当Δ=1+4m<0,即m<-![]() 时,一元二次方程没有实数根,所以
时,一元二次方程没有实数根,所以![]() p是真命题.
p是真命题.
(2)这一命题的否定形式是![]() q:对所有实数x,都有x2+x+1>0.
q:对所有实数x,都有x2+x+1>0.
利用配方法可以验证![]() q是一个真命题.
q是一个真命题.
(3)这一命题的否定形式是![]() r:存在一对等圆,其面积不相等或周长不相等,由平面几何知识知
r:存在一对等圆,其面积不相等或周长不相等,由平面几何知识知![]() r是一个假命题.
r是一个假命题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点(p,q),在|p|≤3,|q|≤3中按均匀分布出现.
(1)点M(x,y)横、纵坐标分别由掷骰子确定,第一次确定横坐标,第二次确定纵坐标,则点M(x,y)落在上述区域的概率?
(2)试求方程x2+2px﹣q2+1=0有两个实数根的概率. -
科目: 来源: 题型:
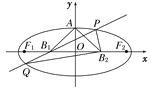
查看答案和解析>>【题目】已知动点M(x,y)到直线l:x=4的距离是它到点N(1,0)的距离的2倍.
(1)求动点M的轨迹C的方程;
(2)过点P(0,3)的直线m与轨迹C交于A,B两点,若A是PB的中点,求直线m的斜率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设{an}是由正数组成的等比数列,公比q=2,且a1a2a3…a30=230 , 那么a3a6a9…a30等于( )
A.210
B.220
C.216
D.215 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
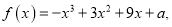 若
若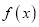 在区间
在区间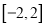 上的最大值为
上的最大值为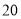 ,求它在该区间上的最小值.
,求它在该区间上的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)是奇函数,并且在R上为增函数,若0≤θ≤
 时,f(msinθ)+f(1﹣m)>0恒成立,则实数m的取值范围是( )
时,f(msinθ)+f(1﹣m)>0恒成立,则实数m的取值范围是( )
A.(0,1)
B.(﹣∞,0)
C.(﹣∞,1)
D.(﹣∞, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义:在数列{an}中,若a
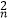 ﹣a
﹣a 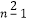 =p(n≥2,n∈N* , p为常数),则称数列{an}为等方差数列,下列判断:
=p(n≥2,n∈N* , p为常数),则称数列{an}为等方差数列,下列判断:
①若{an}是“等方差数列”,则数列{an2}是等差数列;
②{(﹣1)n}是“等方差数列”;
③若{an}是“等方差数列”,则数列{akn}(k∈N* , k为常数)不可能还是“等方差数列”;
④若{an}既是“等方差数列”,又是等差数列,则该数列是常数列.
其中正确的结论是 . (写出所有正确结论的编号)
相关试题

