【题目】已知△ABC中,A,B,C的对边分别是a,b,c,且2cos2 ![]() sinB,a=3c
sinB,a=3c
(Ⅰ)分别求tanC和sin2C的值;
(Ⅱ)若b=1,求△ABC的面积.
参考答案:
【答案】解:(Ⅰ)∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,即:
,即: ![]() ,
,
∴ ![]() 或
或 ![]() (舍),即
(舍),即 ![]() ,
,
∵a=3c,根据正弦定理可得:sinA=3sinC,
∵sin(B+C)=sinA,
∴ ![]() ,
,
经化简得: ![]() ,
,
∴ ![]() .
.
根据基本关系式可计算得: ![]() ,
,
∴ ![]() .
.
(Ⅱ)∵ ![]() ,
,
∴ ![]() ,
,
根据余弦定理及题设可得:  ,
,
解得: ![]() ,
,
∴ ![]()
【解析】(Ⅰ)利用三角函数恒等变换的应用化简 ![]() ,可得
,可得 ![]() ,结合B的范围即可求得
,结合B的范围即可求得 ![]() ,由a=3c,根据正弦定理,三角函数恒等变换的应用化简可得
,由a=3c,根据正弦定理,三角函数恒等变换的应用化简可得 ![]() ,根据基本关系式可计算得sinC,cosC的值,利用倍角公式即可求得sin2C的值.(Ⅱ)由
,根据基本关系式可计算得sinC,cosC的值,利用倍角公式即可求得sin2C的值.(Ⅱ)由 ![]() ,根据余弦定理及题设可解得c,a的值,利用三角形面积公式即可计算求解.
,根据余弦定理及题设可解得c,a的值,利用三角形面积公式即可计算求解.
【考点精析】通过灵活运用正弦定理的定义和余弦定理的定义,掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 即可以解答此题.
即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
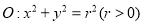 与直线
与直线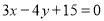 相切.
相切.(1)若直线
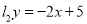 与圆
与圆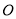 交于
交于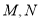 两点,求
两点,求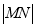 ;
;(2)设圆
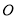 与
与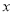 轴的负半轴的交点为
轴的负半轴的交点为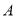 ,过点
,过点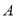 作两条斜率分别为
作两条斜率分别为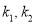 的直线交圆
的直线交圆 于
于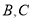 两点,且
两点,且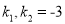 ,试证明直线
,试证明直线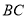 恒过一定点,并求出该定点的坐标.
恒过一定点,并求出该定点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
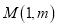 在抛物线
在抛物线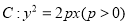 上,且
上,且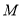 到抛物线
到抛物线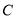 的焦点
的焦点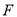 的距离等于2.
的距离等于2.求抛物线
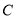 的方程;
的方程;若直线
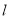 与抛物线
与抛物线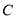 相交于
相交于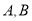 两点,且
两点,且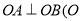 为坐标原点),求证直线
为坐标原点),求证直线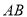 恒过
恒过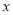 轴上的某定点,并求出该定点坐标.
轴上的某定点,并求出该定点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
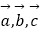 在同一平面内,且
在同一平面内,且 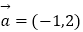 .
.
(1)若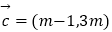 ,且
,且 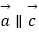 ,求m的值;
,求m的值;
(2)若|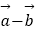 |=3,且
|=3,且 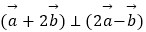 ,求向量
,求向量 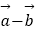 与
与 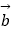 的夹角.
的夹角. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,曲线
中,曲线 :
:  ,曲线
,曲线 :
:  (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点,  轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.(Ⅰ)求曲线
 ,
,  的极坐标方程;
的极坐标方程;(Ⅱ)曲线
 :
:  (
( 为参数,
为参数,  ,
,  )分别交
)分别交 ,
,  于
于 ,
,  两点,当
两点,当 取何值时,
取何值时,  取得最大值.
取得最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某机构为调查2017年下半年落实中学生“阳光体育”活动的情况,设平均每人每天参加体育锻炼时间为
 (单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上,有10000名中学生参加了此项活动,图1是此次调查中某一项的流程图,其输出的结果是6400,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )
(单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上,有10000名中学生参加了此项活动,图1是此次调查中某一项的流程图,其输出的结果是6400,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )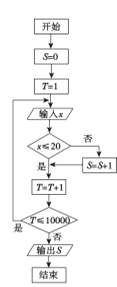
图1
A. 0.64 B. 0.36 C. 6400 D. 3600
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
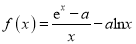 ,其中
,其中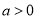 ,
, 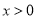 ,
, 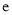 是自然对数的底数.
是自然对数的底数.(Ⅰ)讨论
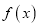 的单调性;
的单调性;(Ⅱ)设函数
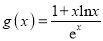 ,证明:
,证明: 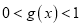 .
.
相关试题

