【题目】已知 ![]() 在同一平面内,且
在同一平面内,且 ![]() .
.
(1)若 ![]() ,且
,且 ![]() ,求m的值;
,求m的值;
(2)若| ![]() |=3,且
|=3,且 ![]() ,求向量
,求向量 ![]() 与
与 ![]() 的夹角.
的夹角.
参考答案:
【答案】
(1)解:由 ![]() ,得:2(m﹣1)+3m=0,解得
,得:2(m﹣1)+3m=0,解得 ![]()
(2)解:因为 ![]() ,所以
,所以 ![]() ,
,
由 ![]() ,得:
,得: ![]() ,
,
∴2 ![]() ﹣2
﹣2 ![]() +3
+3 ![]() =0,即10﹣2
=0,即10﹣2 ![]() +3
+3 ![]() =0,
=0,
由 ![]() ,得
,得 ![]() ,即
,即 ![]() ,
,
解之得, ![]() =2,
=2, ![]() .
.
设 ![]() 与
与 ![]() 的夹角为θ.
的夹角为θ.
则 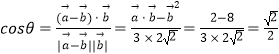 ,
,
又θ∈[0,π],所以 ![]() .
.
即 ![]() 与
与 ![]() 的夹角为
的夹角为 ![]()
【解析】(1)由平面向量的共线定理列方程解出m;(2)分别由两条件列出关于 ![]() 和
和 ![]() 的方程,解出
的方程,解出 ![]() 和
和 ![]() ,代入向量的夹角公式计算.
,代入向量的夹角公式计算.
【考点精析】利用平面向量的坐标运算对题目进行判断即可得到答案,需要熟知坐标运算:设![]() ,
,![]() 则
则![]() ;
;![]() ;设
;设![]() ,则
,则![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了引导居民合理用水,居民生活用水实行二级阶梯式水价计量办法,具体如下:第一阶梯,每户居民月用水量不超过12吨,价格为4元/吨;第二阶梯,每户居民月用水量超过12吨,超过部分的价格为8元/吨.为了了解全市居民月用水量的分布情况,通过抽样获得了100户居民的月用水量(单位:吨),将数据按照
 ,
,  ,…,
,…,  分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.
(图1) (图2)
(Ⅰ)求频率分布直方图中字母
 的值,并求该组的频率;
的值,并求该组的频率;(Ⅱ)通过频率分布直方图,估计该市居民每月的用水量的中位数
 的值(保留两位小数);
的值(保留两位小数);(Ⅲ)如图2是该市居民张某2016年1~6月份的月用水费
 (元)与月份
(元)与月份 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是 . 若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数.
. 若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
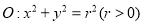 与直线
与直线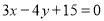 相切.
相切.(1)若直线
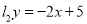 与圆
与圆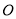 交于
交于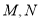 两点,求
两点,求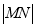 ;
;(2)设圆
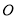 与
与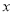 轴的负半轴的交点为
轴的负半轴的交点为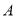 ,过点
,过点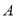 作两条斜率分别为
作两条斜率分别为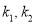 的直线交圆
的直线交圆 于
于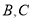 两点,且
两点,且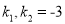 ,试证明直线
,试证明直线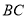 恒过一定点,并求出该定点的坐标.
恒过一定点,并求出该定点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
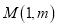 在抛物线
在抛物线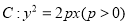 上,且
上,且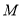 到抛物线
到抛物线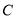 的焦点
的焦点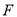 的距离等于2.
的距离等于2.求抛物线
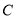 的方程;
的方程;若直线
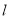 与抛物线
与抛物线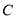 相交于
相交于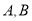 两点,且
两点,且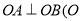 为坐标原点),求证直线
为坐标原点),求证直线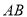 恒过
恒过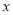 轴上的某定点,并求出该定点坐标.
轴上的某定点,并求出该定点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,A,B,C的对边分别是a,b,c,且2cos2
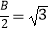 sinB,a=3c
sinB,a=3c
(Ⅰ)分别求tanC和sin2C的值;
(Ⅱ)若b=1,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,曲线
中,曲线 :
:  ,曲线
,曲线 :
:  (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点,  轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.(Ⅰ)求曲线
 ,
,  的极坐标方程;
的极坐标方程;(Ⅱ)曲线
 :
:  (
( 为参数,
为参数,  ,
,  )分别交
)分别交 ,
,  于
于 ,
,  两点,当
两点,当 取何值时,
取何值时,  取得最大值.
取得最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某机构为调查2017年下半年落实中学生“阳光体育”活动的情况,设平均每人每天参加体育锻炼时间为
 (单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上,有10000名中学生参加了此项活动,图1是此次调查中某一项的流程图,其输出的结果是6400,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )
(单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上,有10000名中学生参加了此项活动,图1是此次调查中某一项的流程图,其输出的结果是6400,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )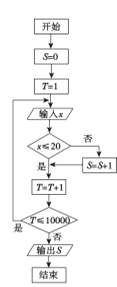
图1
A. 0.64 B. 0.36 C. 6400 D. 3600
相关试题

