【题目】已知直线l:(2 ![]() +1)x+(
+1)x+( ![]() +2)y+2
+2)y+2 ![]() +2=0(
+2=0( ![]() ∈R),有下列四个结论:
∈R),有下列四个结论:
直线l经过定点(0,-2);
②若直线l在x轴和y轴上的截距相等,则 ![]() =1;
=1;
当 ![]() ∈[1, 4+3
∈[1, 4+3 ![]() ]时,直线l的倾斜角q∈[120°,135°];
]时,直线l的倾斜角q∈[120°,135°];
④当 ![]() ∈(0,+∞)时,直线l与两坐标轴围成的三角形面积的最小值为
∈(0,+∞)时,直线l与两坐标轴围成的三角形面积的最小值为 ![]() .
.
其中正确结论的是(填上你认为正确的所有序号).
参考答案:
【答案】③④
【解析】①因为直线l: ![]() 由
由 ![]() 得
得 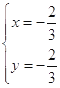 ,
,
所以直线l恒过定点 ![]() ,错;
,错;
②若直线l在x轴和y轴上的截距相等,则其斜率为-1,所以 ![]() ,所以l=1.若直线过原点,在x轴和y轴上的截距均为0,则
,所以l=1.若直线过原点,在x轴和y轴上的截距均为0,则 ![]() ,错.
,错.
③因为直线l的斜率 ![]() ,
,
所以 ![]() ,显然直线l的倾斜角q
,显然直线l的倾斜角q ![]() ,正确.
,正确.
④ ![]() ,
,
设 ![]()
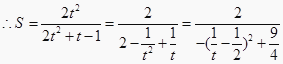 ,
,
当 ![]() 时,S取得最小值,最小值为
时,S取得最小值,最小值为 ![]() .正确.
.正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 中,侧棱垂直于底面,
中,侧棱垂直于底面,  ,
,  ,
,  是棱
是棱 的中点.
的中点.
(Ⅰ)证明:平面
 ⊥平面
⊥平面 ;
;(Ⅱ)求异面直线
 与
与 所成角的余弦值.
所成角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的左右顶点分别为A(﹣2,0),B(2,0),椭圆上除A、B外的任一点C满足kACkBC=﹣
 .
. 
(1)求椭圆C的标准方程;
(2)过点P(4,0)任作一条直线l与椭圆C交于不同的两点M,N,在x轴上是否存在点Q,使得∠PQM+∠PQN=180°?若存在,求出点Q的坐标;若不存在,请说明现由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设A,B是x轴上的两点,点P的横坐标为2,且|PA|=|PB|,若直线PA的方程为x-y+1=0,则直线PB的方程是( ).
A.x+y-5=0
B.2x-y-1=0
C.2y-x-4=0
D.2x+y-7=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】某险种的基本保费为
 (单位:元),继续购买该险峰种的投保人称为续保人,续保人的本年度的保费与其上处度的出险次数的关联如下:
(单位:元),继续购买该险峰种的投保人称为续保人,续保人的本年度的保费与其上处度的出险次数的关联如下:
设该险种一续保人一年内出险次数与相应概率如下:

(1) 求一续保人本年度的保费高于基本保费的概率;
(2) 若一续保人本年度的保费高于基本保费用,求其保费比基本保费高出60%的概率;
(3) 求续保人本年度的平均保费与基本保费的比值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
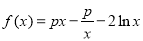 .
.(1)若
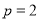 ,求曲线
,求曲线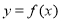 在点
在点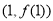 处的切线;
处的切线;(2)若函数
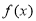 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数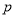 的取值范围;
的取值范围;(3)设函数
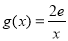 ,若在
,若在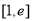 上至少存在一点
上至少存在一点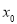 ,使得
,使得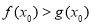 成立,求实数
成立,求实数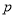 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连接EC、CD.
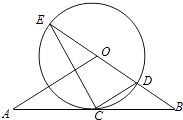
(1)求证:直线AB是⊙O的切线;
(2)若tan∠CED= ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
相关试题

