【题目】某险种的基本保费为![]() (单位:元),继续购买该险峰种的投保人称为续保人,续保人的本年度的保费与其上处度的出险次数的关联如下:
(单位:元),继续购买该险峰种的投保人称为续保人,续保人的本年度的保费与其上处度的出险次数的关联如下:

设该险种一续保人一年内出险次数与相应概率如下:

(1) 求一续保人本年度的保费高于基本保费的概率;
(2) 若一续保人本年度的保费高于基本保费用,求其保费比基本保费高出60%的概率;
(3) 求续保人本年度的平均保费与基本保费的比值.
参考答案:
【答案】(1)0.55;(2) ![]() ;(3)1.23.
;(3)1.23.
【解析】试题分析:
(1)利用概率的性质可得一续保人本年度的保费高于基本保费的概率是0.55;
(2)结合条件概率计算公式可得一续保人本年度的保费高于基本保费用,求其保费比基本保费高出60%的概率是![]() ;
;
(3)首项列出分布列,然后结合分布列计算可得续保人本年度的平均保费与基本保费的比值是1.23.
试题解析:
(1) 设![]() 表示事件:“一续保人本年度的保费高于基本保费”,则事件
表示事件:“一续保人本年度的保费高于基本保费”,则事件![]() 发生当且仅当一年内出险次数大于1,故
发生当且仅当一年内出险次数大于1,故![]()
(2) 设![]() 表示事件:“一续保人本年度的保费比基本保费高出60%”,则事件
表示事件:“一续保人本年度的保费比基本保费高出60%”,则事件![]() 发生当且仅当一年内出险次数大于3,故
发生当且仅当一年内出险次数大于3,故![]()
又![]() ,故
,故![]() ,因此所求的概率为
,因此所求的概率为![]()
(3)记续保人本年度的保费为![]() ,则
,则![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
| 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
![]() ,因此续保人本年度的平均保费与基本保费的比值为
,因此续保人本年度的平均保费与基本保费的比值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的左右顶点分别为A(﹣2,0),B(2,0),椭圆上除A、B外的任一点C满足kACkBC=﹣
 .
. 
(1)求椭圆C的标准方程;
(2)过点P(4,0)任作一条直线l与椭圆C交于不同的两点M,N,在x轴上是否存在点Q,使得∠PQM+∠PQN=180°?若存在,求出点Q的坐标;若不存在,请说明现由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设A,B是x轴上的两点,点P的横坐标为2,且|PA|=|PB|,若直线PA的方程为x-y+1=0,则直线PB的方程是( ).
A.x+y-5=0
B.2x-y-1=0
C.2y-x-4=0
D.2x+y-7=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l:(2
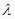 +1)x+(
+1)x+( 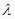 +2)y+2
+2)y+2 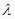 +2=0(
+2=0( 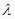 ∈R),有下列四个结论:
∈R),有下列四个结论:
直线l经过定点(0,-2);
②若直线l在x轴和y轴上的截距相等,则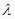 =1;
=1;
当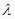 ∈[1, 4+3
∈[1, 4+3 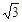 ]时,直线l的倾斜角q∈[120°,135°];
]时,直线l的倾斜角q∈[120°,135°];
④当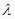 ∈(0,+∞)时,直线l与两坐标轴围成的三角形面积的最小值为
∈(0,+∞)时,直线l与两坐标轴围成的三角形面积的最小值为 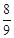 .
.
其中正确结论的是(填上你认为正确的所有序号). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
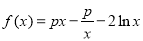 .
.(1)若
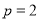 ,求曲线
,求曲线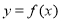 在点
在点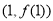 处的切线;
处的切线;(2)若函数
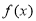 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数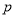 的取值范围;
的取值范围;(3)设函数
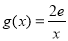 ,若在
,若在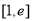 上至少存在一点
上至少存在一点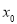 ,使得
,使得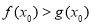 成立,求实数
成立,求实数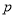 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连接EC、CD.
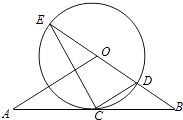
(1)求证:直线AB是⊙O的切线;
(2)若tan∠CED= ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:sinθ=ρcos2θ,过点M(﹣1,2)的直线l:
 (t为参数)与曲线C相交于A、B两点.求:
(t为参数)与曲线C相交于A、B两点.求:
(1)线段AB的长度;
(2)点M(﹣1,2)到A、B两点的距离之积.
相关试题

