【题目】已知关于x的方程2x2﹣( ![]() +1)x+m=0的两根为sinθ和cosθ,θ∈(0,π).求:
+1)x+m=0的两根为sinθ和cosθ,θ∈(0,π).求:
(1)m的值;
(2)![]() +
+ ![]() 的值;
的值;![]()
(3)方程的两根及此时θ的值.
参考答案:
【答案】
(1)
解:∵sinθ,cosθ是方程2x2﹣( ![]() +1)x+m=0的两个根,
+1)x+m=0的两个根,
∴sinθ+cosθ= ![]() ,sinθcosθ=
,sinθcosθ= ![]()
则(sinθ+cosθ)2=1+2sinθcosθ=1+m= ![]()
∴m= ![]() ;
;
(2)
解: ![]() +
+ ![]() =
= ![]() =sinθ+cosθ=
=sinθ+cosθ= ![]()
(3)
解:由(1)知,sinθ+cosθ= ![]() ,sinθcosθ=
,sinθcosθ= ![]()
∴sinθ= ![]() ,cosθ=
,cosθ= ![]() 或sinθ=
或sinθ= ![]() ,cosθ=
,cosθ= ![]() ,
,
∵θ∈(0,π),
∴θ= ![]() 或
或 ![]()
【解析】(1)由sinθ,cosθ是方程2x2﹣( ![]() +1)x+m=0的两个根,根据韦达定理(一元二次方程根与系数的关系)我们易得:sinθ+cosθ=
+1)x+m=0的两个根,根据韦达定理(一元二次方程根与系数的关系)我们易得:sinθ+cosθ= ![]() ,sinθcosθ=
,sinθcosθ= ![]() ,结合同角三角函数平方关系,根据一个关于m的方程,解方程即可得到答案;(2)切化弦,代入计算可得结论;(3)由(1)知,sinθ+cosθ=
,结合同角三角函数平方关系,根据一个关于m的方程,解方程即可得到答案;(2)切化弦,代入计算可得结论;(3)由(1)知,sinθ+cosθ= ![]() ,sinθcosθ=
,sinθcosθ= ![]() ,可得sinθ=
,可得sinθ= ![]() ,cosθ=
,cosθ= ![]() 或sinθ=
或sinθ= ![]() ,cosθ=
,cosθ= ![]() ,从而可求θ的值.
,从而可求θ的值.
【考点精析】解答此题的关键在于理解同角三角函数基本关系的运用的相关知识,掌握同角三角函数的基本关系:![]()
![]() ;
;![]()
![]() ;(3) 倒数关系:
;(3) 倒数关系:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的两个焦点是F1(﹣2,0),F2(2,0),且椭圆C经过点A(0,
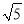 ).
).(1)求椭圆C的标准方程;
(2)若过椭圆C的左焦点F1(﹣2,0)且斜率为1的直线l与椭圆C交于P、Q两点,求线段PQ的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.(本小题满分12分)
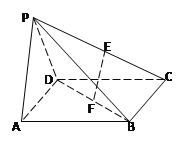
如图,四棱锥P—ABCD中,底面ABCD是边长为
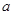 的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=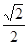 AD.
AD.(Ⅰ)求证:EF//平面PAD;
(Ⅱ)求三棱锥C—PBD的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
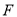 是拋物线
是拋物线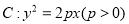 的焦点, 若点
的焦点, 若点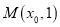 在
在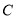 上,且
上,且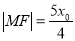 .
.(1)求
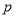 的值;
的值;(2)若直线
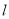 经过点
经过点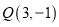 且与
且与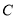 交于
交于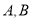 (异于
(异于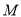 )两点, 证明: 直线
)两点, 证明: 直线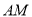 与直线
与直线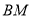 的斜率之积为常数.
的斜率之积为常数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成
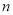 小块地,在总共
小块地,在总共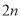 小块地中,随机选
小块地中,随机选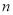 小块地种植品种甲,另外
小块地种植品种甲,另外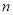 小块地种植品种乙.
小块地种植品种乙.(1)假设
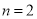 ,求第一大块地都种植品种甲的概率;
,求第一大块地都种植品种甲的概率;(2)试验时每大块地分成
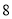 小块,即
小块,即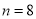 ,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:
,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:甲
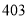
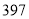
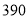
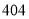
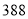
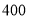
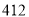
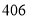
乙
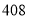
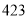
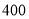
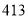
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂有4台大型机器,在一个月中,一台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修,每台机器出现故障需要维修的概率为
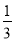 .
.(1)若出现故障的机器台数为
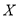 ,求
,求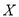 的分布列;
的分布列;(2) 该厂至少有多少名工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不少于90%?
(3)已知一名工人每月只有维修1台机器的能力,每月需支付给每位工人1万元的工资,每台机器不出现故障或出现故障能及时维修,就使该厂产生5万元的利润,否则将不产生利润,若该厂现有2名工人,求该厂每月获利的均值.
-
科目: 来源: 题型:
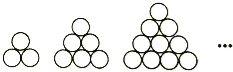
查看答案和解析>>【题目】宋元时期杰出的数学家朱世杰在其数学巨著《四元玉鉴》卷中“茭草形段”第一个问题“今有茭草六百八十束,欲令‘落一形’埵(同垛)之.问底子(每层三角形边茭草束数,等价于层数)几何?”中探讨了“垛枳术”中的落一形垛(“落一形”即是指顶上1束,下一层3束,再下一层6束,…,成三角锥的堆垛,故也称三角垛,如图,表示第二层开始的每层茭草束数),则本问题中三角垛底层茭草总束数为 .
相关试题

