【题目】如图,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,四边形
,四边形![]() 是菱形,
是菱形, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() 交于点
交于点![]() ,
, ![]() 是
是![]() 上任意一点.
上任意一点.
(1)求证: ![]() ;
;
(2)已知二面角![]() 的余弦值为
的余弦值为![]() ,若
,若![]() 为
为![]() 的中点,求
的中点,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)线线垂直问题转化为线面问题即可解决,即![]()
![]() ,由
,由![]() 平面
平面![]() ,得
,得![]() ,又分析可知
,又分析可知![]() ,且
,且![]() ,所以
,所以![]() (2)解法1:(空间向量在立体几何中的应用)设
(2)解法1:(空间向量在立体几何中的应用)设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,即
,即![]() 与平面
与平面![]() 所成角为
所成角为![]() 与平面
与平面![]() 的法向量
的法向量![]() 所成角,如图所示的空间直角坐标系,
所成角,如图所示的空间直角坐标系,
设![]() 则
则![]() ,
, ![]() ,
,
平面![]() 的一个法向量为
的一个法向量为![]() (1,0,0),
(1,0,0),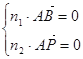 ,得到
,得到
再由二面角![]() 的余弦值为
的余弦值为![]() ,
, 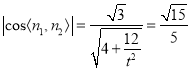 ,解得
,解得![]() ,
,
故![]() ,
, ![]() ,最后
,最后![]() 求得;
求得;
解法2:通过构造法作出二面角![]() 的平面角
的平面角![]() ,
,
设DP=t, 作出二面角![]() 的平面角
的平面角![]() ,
,
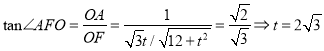
由![]() ,求出点
,求出点![]() 到平面
到平面![]() 的距离
的距离![]()
![]()
试题解析:(1)因为![]() 平面
平面![]() ,所以
,所以![]() , 1分
, 1分
因为四边形![]() 为菱形,所以
为菱形,所以![]() 2分
2分
又![]()
因为![]() 5分
5分
(2)解法1:
连接![]() 在
在![]() 中,
中, ![]()
所以![]() 分别以
分别以![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
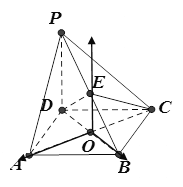
设![]() 则
则![]() ,
, ![]() . 6分
. 6分
由(1)知,平面![]() 的一个法向量为
的一个法向量为![]() (1,0,0), 设平面
(1,0,0), 设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则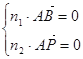 得
得 ,令
,令![]() ,得
,得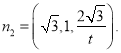 8分
8分
因为二面角![]() 的余弦值为
的余弦值为![]() ,所以
,所以 ,
,
解得![]() 或
或![]() (舍去),所以
(舍去),所以![]() 10分
10分
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .因为
.因为![]() ,
, ![]() ,
,
∴![]()
所以![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() . 12分
. 12分
解法2:
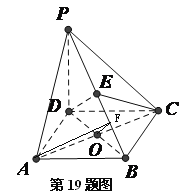
设DP=t, 作出二面角![]() 的平面角
的平面角![]()
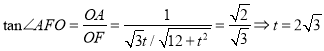
![]() 由
由![]() ,求出点
,求出点![]() 到平面
到平面![]() 的距离
的距离![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某港口有一个泊位,现统计了某月100艘轮船在该泊位停靠的时间(单位:小时),如果停靠时间不足半小时按半小时计时,超过半小时不足1小时按1小时计时,以此类推,统计结果如表:
停靠时间
2.5
3
3.5
4
4.5
5
5.5
6
轮船数量
12
12
17
20
15
13
8
3
(Ⅰ)设该月100艘轮船在该泊位的平均停靠时间为
 小时,求
小时,求 的值;
的值;(Ⅱ)假定某天只有甲、乙两艘轮船需要在该泊位停靠
 小时,且在一昼夜的时间段中随机到达,求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率.
小时,且在一昼夜的时间段中随机到达,求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】
 是等边三角形,边长为4,
是等边三角形,边长为4, 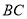 边的中点为
边的中点为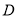 ,椭圆
,椭圆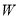 以
以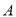 ,
, 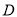 为左、右两焦点,且经过
为左、右两焦点,且经过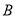 、
、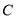 两点。
两点。(1)求该椭圆的标准方程;
(2)过点
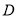 且
且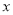 轴不垂直的直线
轴不垂直的直线 交椭圆于
交椭圆于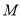 ,
, 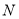 两点,求证:直线
两点,求证:直线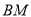 与
与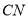 的交点在一条定直线上.
的交点在一条定直线上. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时,  .
.(1)直接写出函数
 的增区间(不需要证明);
的增区间(不需要证明);(2)求出函数
 ,
,  的解析式;
的解析式;(3)若函数
 ,
,  ,求函数
,求函数 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系,将曲线
 上的每一个点的横坐标保持不变,纵坐标缩短为原来的
上的每一个点的横坐标保持不变,纵坐标缩短为原来的 ,得到曲线
,得到曲线 ,以坐标原点
,以坐标原点 为极点,
为极点,  轴的正半轴为极轴,建立极坐标系,
轴的正半轴为极轴,建立极坐标系,  的极坐标方程为
的极坐标方程为 .
.(Ⅰ)求曲线
 的参数方程;
的参数方程;(Ⅱ)过原点
 且关于
且关于 轴对称的两条直线
轴对称的两条直线 与
与 分别交曲线
分别交曲线 于
于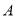 、
、 和
和 、
、 ,且点
,且点 在第一象限,当四边形
在第一象限,当四边形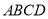 的周长最大时,求直线
的周长最大时,求直线 的普通方程.
的普通方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年“一带一路”国际合作高峰论坛于今年5月14日至15日在北京举行.为高标准完成高峰论坛会议期间的志愿服务工作,将从27所北京高校招募大学生志愿者,某调查机构从是否有意愿做志愿者在某高校访问了80人,经过统计,得到如下丢失数据的列联表:(
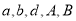 ,表示丢失的数据)
,表示丢失的数据)无意愿
有意愿
总计
男
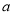
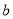
40
女
5
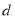
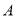
总计
25
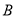
80
(1)求出
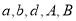 的值,并判断:能否有99.9%的把握认为有意愿做志愿者与性别有关;
的值,并判断:能否有99.9%的把握认为有意愿做志愿者与性别有关;(2)若表中无意愿做志愿者的5个女同学中,3个是大学三年级同学,2个是大学四年级同学.现从这5个同学中随机选2同学进行进一步调查,求这2个同学是同年级的概率.
附参考公式及数据:
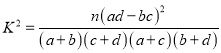 ,其中
,其中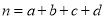 .
.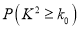
0.40
0.25
0.10
0.010
0.005
0.001
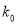
0.708
1.323
2.706
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人为了响应政府“节能减排”的号召,决定各购置一辆纯电动汽车.经了解目前市场上销售的主流纯电动汽车,按续驶里程数
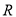 (单位:公里)可分为三类车型,
(单位:公里)可分为三类车型, 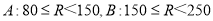 ,
, 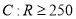 .甲从
.甲从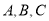 三类车型中挑选,乙从
三类车型中挑选,乙从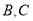 两类车型中挑选,甲、乙两人选择各类车型的概率如表:
两类车型中挑选,甲、乙两人选择各类车型的概率如表: 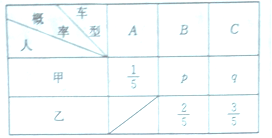
已知甲、乙都选
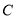 类型的概率为
类型的概率为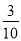 .
.(1)求
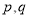 的值;
的值; (2)求甲、乙选择不同车型的概率;
(3)某市对购买纯电动汽车进行补贴,补贴标准如下表:

记甲、乙两人购车所获得的财政补贴之和为
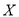 ,求
,求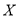 的分布列和数学期望.
的分布列和数学期望.
相关试题

