【题目】如图,在四棱锥P﹣ABCD中,侧面PAB⊥底面ABCD,且∠PAB=∠ABC=90°,AD∥BC,PA=AB=BC=2AD,E是PC的中点.
(Ⅰ)求证:DE⊥平面PBC;
(Ⅱ)求二面角A﹣PD﹣E的余弦值.
参考答案:
【答案】(Ⅰ)证明:∵侧面PAB⊥底面ABCD,且∠PAB=∠ABC=90°,AD∥BC,
∴PA⊥AB,PA⊥AD⊥AD⊥AB,
以点A为坐标原点,建立如图所示的坐标系,设PA=AB=BC=2AD=2,则P(0,0,2),D(1,0,0),B(0,2,0),C(2,2,0),E(1,1,1),
∴ ![]() =(0,1,1),
=(0,1,1), ![]() =(0,2,﹣2),
=(0,2,﹣2), ![]() =(2,2,﹣2),
=(2,2,﹣2),
∴ ![]() =0,
=0, ![]() =0,
=0,
∴DE⊥PB,DE⊥PC,
∵PB∩PC=P,
∴DE⊥平面PBC;
(Ⅱ)解:由(Ⅰ)可知平面PAD的一个法向量 ![]() =(0,2,0).
=(0,2,0).
设平面PCD的一个法向量为 ![]() =(x,y,z),则
=(x,y,z),则
∵ ![]() =(1,0,﹣2),
=(1,0,﹣2), ![]() =(2,2,﹣2),
=(2,2,﹣2),
∴ ![]() ,
,
∴取 ![]() =(2,﹣1,1),
=(2,﹣1,1),
∴cos< ![]() ,
, ![]() >=
>= ![]() =﹣
=﹣ ![]() .
.
【解析】(Ⅰ)以点A为坐标原点,建立坐标系,证明 ![]() =0,
=0, ![]() =0,即可证明DE⊥平面PBC;(Ⅱ)求出平面PAD的一个法向量、平面PCD的一个法向量,利用向量的夹角公式,即可求二面角A﹣PD﹣E的余弦值.
=0,即可证明DE⊥平面PBC;(Ⅱ)求出平面PAD的一个法向量、平面PCD的一个法向量,利用向量的夹角公式,即可求二面角A﹣PD﹣E的余弦值.
【考点精析】根据题目的已知条件,利用直线与平面垂直的判定的相关知识可以得到问题的答案,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某住宅小区的平面图呈圆心角
 为的扇形
为的扇形 ,小区的两个出入口设置在点
,小区的两个出入口设置在点 及点
及点 处,且小区里有一条平行于
处,且小区里有一条平行于 的小路
的小路 。
。
(1)已知某人从
 沿
沿 走到
走到 用了
用了 分钟,从
分钟,从 沿
沿 走到
走到 用了
用了 分钟,若此人步行的速度为每分钟
分钟,若此人步行的速度为每分钟 米,求该扇形的半径
米,求该扇形的半径 的长(精确到
的长(精确到 米)
米) (2)若该扇形的半径为
 ,已知某老人散步,从
,已知某老人散步,从 沿
沿 走到
走到 ,再从
,再从 沿
沿 走到
走到 ,试确定
,试确定 的位置,使老人散步路线最长。
的位置,使老人散步路线最长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:



按此规律,第
 个等式可为__________.
个等式可为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者。现从符合条件的志愿者中 随机抽取
 名按年龄分组:第
名按年龄分组:第 组
组 ,第
,第 组
组 ,第
,第 组
组 ,第
,第 组
组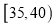 ,第
,第 组
组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)若从第
 ,
, ,
, 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取 名志愿者参广场的宣传活动,应从第
名志愿者参广场的宣传活动,应从第 ,
, ,
, 组各抽取多少名志愿者?
组各抽取多少名志愿者?(2)在(1)的条件下,该市决定在这
 名志愿者中随机抽取
名志愿者中随机抽取 名志愿者介绍宣传经验,求第
名志愿者介绍宣传经验,求第 组志愿者有被抽中的概率.
组志愿者有被抽中的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 处有一港口,两艘海轮
处有一港口,两艘海轮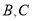 同时从港口
同时从港口 处出发向正北方向匀速航行,海轮
处出发向正北方向匀速航行,海轮 的航行速度为20海里/小时,海轮
的航行速度为20海里/小时,海轮 的航行速度大于海轮
的航行速度大于海轮 .在港口
.在港口 北偏东60°方向上的
北偏东60°方向上的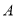 处有一观测站,1小时后在
处有一观测站,1小时后在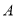 处测得与海轮
处测得与海轮 的距离为30海里,且
的距离为30海里,且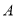 处对两艘海轮
处对两艘海轮 ,
, 的视角为30°.
的视角为30°.
(1)求观测站
 到港口
到港口 的距离;
的距离;(2)求海轮
 的航行速度.
的航行速度. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查喜欢看书是否与性别有关,某校调查小组就“是否喜欢看书”这个问题,在全校随机调研了100名学生.
(1)完成下列
 列联表:
列联表:喜欢看书
不喜欢看书
合计
女生
15
50
男生
25
合计
100
(2)能否在犯错率不超过0.025的前提下认为“喜欢看书与性别有关”.
附:
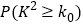
0.15
0.10
0.05
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5024
6.635
7.879
10.828
(参考公式:
 ,其中
,其中 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】二项式
 的二项式系数和为256.
的二项式系数和为256.(1)求展开式中二项式系数最大的项;
(2)求展开式中各项的系数和;
(3)展开式中是否有有理项,若有,求系数;若没有,说明理由.
相关试题

