【题目】椭圆![]() 过点
过点![]() ,离心率为
,离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,过
,过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点.
两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)当![]() 的面积为
的面积为![]() 时,求直线的方程.
时,求直线的方程.
参考答案:
【答案】(1)![]() ;(2)直线方程为:
;(2)直线方程为:![]() 或
或![]() .
.
【解析】
试题分析:本题主要考查椭圆的标准方程及其几何性质、直线的标准方程、直线与椭圆相交问题、三角形面积公式等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,由于椭圆过点A,将A点坐标代入得到a和b的关系式,再利用椭圆的离心率得到a与c的关系式,从而求出a和b,得到椭圆的标准方程;第二问,过![]() 的直线有特殊情况,即当直线的倾斜角为
的直线有特殊情况,即当直线的倾斜角为![]() 时,先讨论,再讨论斜率不不为
时,先讨论,再讨论斜率不不为![]() 的情况,将直线方程与椭圆方程联立,利用韦达定理得到
的情况,将直线方程与椭圆方程联立,利用韦达定理得到![]() 和
和![]() ,代入到三角形面积公式中,解出k的值,从而得到直线方程.
,代入到三角形面积公式中,解出k的值,从而得到直线方程.
试题解析:(1)因为椭圆![]() 过点
过点![]() ,所以
,所以![]() ①,又因为离心率为
①,又因为离心率为![]() ,所以
,所以![]() ,所以
,所以![]() ②,解①②得
②,解①②得![]() .
.
所以椭圆的方程为:![]() (4分)
(4分)
(2)①当直线的倾斜角为![]() 时,
时,![]() ,
,
![]() ,不适合题意。 (6分)
,不适合题意。 (6分)
②当直线的倾斜角不为![]() 时,设直线方程
时,设直线方程![]() ,
,
代入![]() 得:
得:![]() (7分)
(7分)
设![]() ,则
,则![]() ,
,![]() ,
,

![]() ,
,
所以直线方程为:![]() 或
或![]() (12分)
(12分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
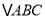 中,角
中,角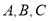 的对边分别为
的对边分别为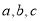 ,若
,若 (
(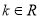 ).
).(1)判断
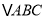 的形状;
的形状;(2)若
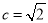 ,求
,求 的值.
的值. -
科目: 来源: 题型:
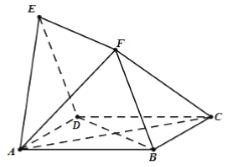
查看答案和解析>>【题目】如图,四边形
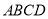 与
与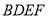 均为菱形,
均为菱形,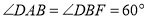 ,且
,且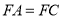 .
.
(1)求证:
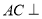 平面
平面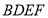 ;
;(2)求证:
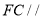 平面
平面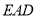 ;
;(3)求二面角
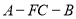 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
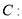

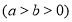 的离心率为
的离心率为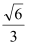 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为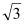 .
.(1) 求椭圆
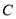 的方程;
的方程;(2) 设直线
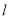 与椭圆
与椭圆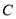 交于
交于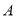 、
、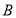 两点,坐标原点
两点,坐标原点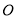 到直线
到直线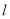 的距离为
的距离为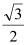 ,求
,求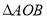 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 在
在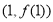 处的切线方程为
处的切线方程为 .
.(1)求
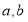 的值;
的值;(2)求函数
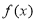 的极值.
的极值.(3)若
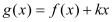 在
在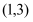 是单调函数,求
是单调函数,求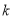 的取值范围
的取值范围 -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂有容量300吨的水塔一个,每天从早六点到晚十点供应生活和生产用水,已知:该厂生活用水每小时10吨,工业用水总量
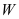 (吨)与时间
(吨)与时间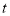 (单位:小时,规定早晨六点时
(单位:小时,规定早晨六点时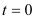 )的函数关系为
)的函数关系为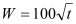 ,水塔的进水量有10级,第一级每小时进水10吨,以后每提高一级, 进水量增加10吨.若某天水塔原有水100吨,在供应同时打开进水管.问该天进水量应选择几级,既能保证该厂用水(即水塔中水不空),又不会使水溢出?
,水塔的进水量有10级,第一级每小时进水10吨,以后每提高一级, 进水量增加10吨.若某天水塔原有水100吨,在供应同时打开进水管.问该天进水量应选择几级,既能保证该厂用水(即水塔中水不空),又不会使水溢出? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{
 }的前n项和
}的前n项和 (n为正整数)。
(n为正整数)。(1)令
 ,求证数列{
,求证数列{ }是等差数列,并求数列{
}是等差数列,并求数列{ }的通项公式;
}的通项公式;(2)令
 ,
,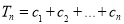 试比较
试比较 与
与 的大小,并予以证明.
的大小,并予以证明.
相关试题

