【题目】某厂有容量300吨的水塔一个,每天从早六点到晚十点供应生活和生产用水,已知:该厂生活用水每小时10吨,工业用水总量![]() (吨)与时间
(吨)与时间![]() (单位:小时,规定早晨六点时
(单位:小时,规定早晨六点时![]() )的函数关系为
)的函数关系为![]() ,水塔的进水量有10级,第一级每小时进水10吨,以后每提高一级, 进水量增加10吨.若某天水塔原有水100吨,在供应同时打开进水管.问该天进水量应选择几级,既能保证该厂用水(即水塔中水不空),又不会使水溢出?
,水塔的进水量有10级,第一级每小时进水10吨,以后每提高一级, 进水量增加10吨.若某天水塔原有水100吨,在供应同时打开进水管.问该天进水量应选择几级,既能保证该厂用水(即水塔中水不空),又不会使水溢出?
参考答案:
【答案】进水选择4级
【解析】
试题分析:设进水选择第![]() 级,在
级,在![]() 时刻水塔中的水容量
时刻水塔中的水容量![]() 等于原有的水加进水量,减生活用水和工业用水,即
等于原有的水加进水量,减生活用水和工业用水,即![]() ,
,![]() ,当
,当![]() 时,求解
时,求解![]() 的取值范围.
的取值范围.
试题解析:设水塔进水量选择第![]() 级,在
级,在![]() 时刻水塔中的水容量
时刻水塔中的水容量![]() 等于水塔中的存水量100吨加进水量
等于水塔中的存水量100吨加进水量![]() 吨,减去生产用水
吨,减去生产用水![]() 吨,在减去工业用水
吨,在减去工业用水![]() 吨,即
吨,即![]() (
(![]() );
);
若水塔中的水量既能保证该厂用水,又不会使水溢出,则一定有![]() .
.
即![]() ,
,
所以![]() 对一切
对一切![]() 恒成立.
恒成立.
因为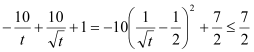 ,
,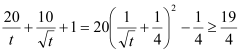 ,
,
所以![]() ,即
,即![]() .即进水选择4级.
.即进水选择4级.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
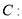

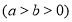 的离心率为
的离心率为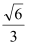 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为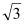 .
.(1) 求椭圆
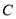 的方程;
的方程;(2) 设直线
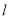 与椭圆
与椭圆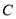 交于
交于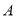 、
、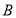 两点,坐标原点
两点,坐标原点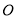 到直线
到直线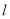 的距离为
的距离为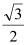 ,求
,求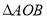 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
 过点
过点 ,离心率为
,离心率为 ,左、右焦点分别为
,左、右焦点分别为 ,过
,过 的直线交椭圆于
的直线交椭圆于 两点.
两点.(Ⅰ)求椭圆C的方程;
(Ⅱ)当
 的面积为
的面积为 时,求直线的方程.
时,求直线的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 在
在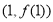 处的切线方程为
处的切线方程为 .
.(1)求
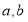 的值;
的值;(2)求函数
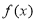 的极值.
的极值.(3)若
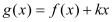 在
在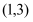 是单调函数,求
是单调函数,求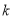 的取值范围
的取值范围 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{
 }的前n项和
}的前n项和 (n为正整数)。
(n为正整数)。(1)令
 ,求证数列{
,求证数列{ }是等差数列,并求数列{
}是等差数列,并求数列{ }的通项公式;
}的通项公式;(2)令
 ,
,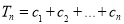 试比较
试比较 与
与 的大小,并予以证明.
的大小,并予以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
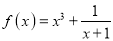 ,
, 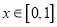 .
.(1)证明:
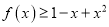 ;
;(2)根据(1)证明:
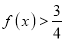 .
.(B)已知函数
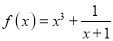 ,
, 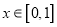 .
.(1)用分析法证明:
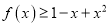 ;
;(2)证明:
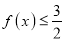 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】等比数列
 的前
的前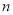 项和为
项和为 ,已知对任意的
,已知对任意的 ,点
,点 均在函数
均在函数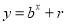 (
( 且
且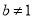 ,
,  均为常数)的图象上.
均为常数)的图象上.
(1)求 的值;
的值;(2)当
 时,记
时,记 ,证明:对任意的
,证明:对任意的 ,不等式
,不等式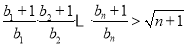 成立.
成立.
相关试题

