【题目】我国西部某省4A级风景区内住着一个少数民族村,该村投资了800万元修复和加强民俗文化基础设施,据调查,修复好村民俗文化基础设施后,任何一个月内(每月按30天计算)每天的旅游人数f(x)与第x天近似地满足![]() (千人),且参观民俗文化村的游客人均消费g(x)近似地满足g(x)=143﹣|x﹣22|(元).
(千人),且参观民俗文化村的游客人均消费g(x)近似地满足g(x)=143﹣|x﹣22|(元).
(1)求该村的第x天的旅游收入p(x)(单位千元,1≤x≤30,x∈N*)的函数关系;
(2)若以最低日收入的20%作为每一天的计量依据,并以纯收入的5%的税率收回投资成本,试问该村在两年内能否收回全部投资成本?
参考答案:
【答案】(1)见解析(2)该村在两年内能收回全部投资成本.
【解析】试题分析:(1)依题意有![]()
![]() .去绝对值化为
.去绝对值化为 ;(2)①当
;(2)①当![]() ,
, ![]() 时,利用基本不等式求得最小值为
时,利用基本不等式求得最小值为![]() .②当
.②当![]() ,
, ![]() 时,利用单调性求得最小值为
时,利用单调性求得最小值为![]() ,所以日收益最低为
,所以日收益最低为![]() 千元,由此计算得两年收益
千元,由此计算得两年收益![]() ,所以可以收回成本.
,所以可以收回成本.
试题解析:
(1)依题意有![]()
![]()
 .
.
(2)①当![]() ,
, ![]() 时,
时,
![]() (当且仅当
(当且仅当![]() 时,等号成立),
时,等号成立),
∴![]() (千元)②当
(千元)②当![]() ,
, ![]() 时,
时, ![]() ,
,
考察函数![]() ,可知函数
,可知函数![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() (千元),
(千元),
又![]() ,∴日最低收入为1116千元.
,∴日最低收入为1116千元.
该村两年可收回的投资资金为![]() (千元)
(千元)![]() (万元).
(万元).
∵![]() (万元)
(万元)![]() (万元),∴该村在两年内能收回全部投资成本.
(万元),∴该村在两年内能收回全部投资成本.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 平行于同一个平面的两个平面平行
B. 平行于同一直线的两个平面平行
C. 垂直于同一个平面的两条直线平行
D. 垂直于同一条直线的两个平面平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的图象过点
的图象过点 ,且在点
,且在点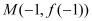 处的切线方程
处的切线方程 .
.(1)求函数
 的解析式;
的解析式;(2)求函数
 与
与 的图像有三个交点,求
的图像有三个交点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(2)是否存在整数
 ,使得关于
,使得关于 的不等式
的不等式 的解集为
的解集为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】两个球的体积之比为8:27,那么这两个球的表面积之比为( )
A. 2:3 B. 4:9 C. 8:27 D. 16:81
-
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
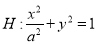 (
(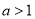 ),原点
),原点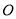 到直线
到直线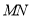 的距离为
的距离为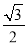 ,其中:点
,其中:点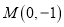 ,点
,点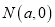 .
.(1)求该椭圆
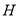 的离心率
的离心率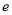 ;
;(2)经过椭圆右焦点
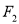 的直线
的直线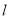 和该椭圆交于
和该椭圆交于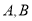 两点,点
两点,点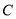 在椭圆上,
在椭圆上, 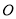 为原点,若
为原点,若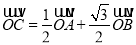 ,求直线
,求直线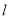 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, 
 平面
平面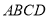 ,
,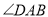 为直角,
为直角,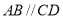 ,
, ,
,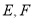 分别为
分别为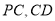 的中点.
的中点.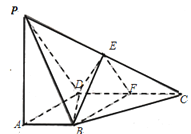
(Ⅰ)证明:
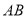
 平面
平面 ;
;(Ⅱ)若
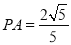 ,求二面角
,求二面角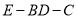 .
.
相关试题

