【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线![]() 上的点
上的点 对应的参数
对应的参数![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若点![]() ,
, ![]() 在曲线
在曲线![]() 上,求
上,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)将![]() ,代入
,代入![]() ,得
,得![]() 再利用同角三角函数关系消去参数得
再利用同角三角函数关系消去参数得![]() .由题意可设圆
.由题意可设圆![]() 的方程
的方程![]() ,将点
,将点![]() 代入可得
代入可得![]() ,即得
,即得![]() 的方程为
的方程为![]() ,(2)先将
,(2)先将![]() 直角坐标方程化为极坐标方程:
直角坐标方程化为极坐标方程: ![]() ,再将点
,再将点![]() ,
, ![]() 代入解得
代入解得![]() ,最后计算
,最后计算![]() 的值.
的值.
试题解析:解:(Ⅰ)将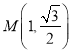 及对应的参数
及对应的参数![]() ,代入
,代入![]() ,得
,得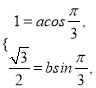 即
即![]()
∴曲线![]() 的方程为
的方程为![]() (
(![]() 为参数),或
为参数),或![]() .
.
设圆![]() 的半径为
的半径为![]() ,由题意,圆
,由题意,圆![]() 的方程
的方程![]() ,(或
,(或![]() ).
).
将点![]() 代入
代入![]() ,得
,得![]() ,即
,即![]() ,
,
所以曲线![]() 的方程为
的方程为![]() 或
或![]() .
.
(Ⅱ)因为点![]() ,
, ![]() 在曲线
在曲线![]() 上,
上,
所以![]() ,
, ![]() ,
,
所以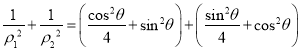
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
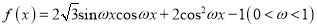 ,直线
,直线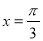 是函数
是函数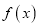 图象的一条对称轴.
图象的一条对称轴.(1)求
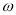 的值,并求
的值,并求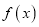 的解析式;
的解析式;(2)若关于
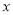 的方程
的方程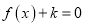 在区间
在区间 上有且只有一个实数解,求实数
上有且只有一个实数解,求实数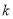 的取值范围;
的取值范围;(3)已知函数
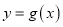 的图象是由
的图象是由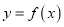 图象上的所有点的横坐标伸长到原来的2倍,然后再向左平移
图象上的所有点的横坐标伸长到原来的2倍,然后再向左平移 个单位得到,若
个单位得到,若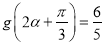 ,
, 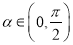 ,求
,求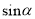 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】四名同学根据各自的样本数据研究变量
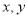 之间的相关关系,并求得回归直线方程和相关系数
之间的相关关系,并求得回归直线方程和相关系数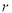 ,分别得到以下四个结论:
,分别得到以下四个结论: ①
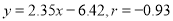 ②
②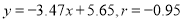
③
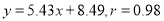 ④
④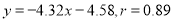
其中,一定不正确的结论序号是( )
A. ②③ B. ①④ C. ①②③ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
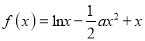 ,
, 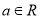 .
.(Ⅰ)当
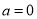 时,求函数
时,求函数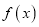 在
在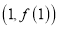 处的切线方程;
处的切线方程;(Ⅱ)令
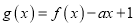 ,求函数
,求函数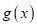 的极值;
的极值;(Ⅲ)若
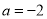 ,正实数
,正实数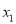 ,
, 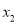 满足
满足 ,证明:
,证明: 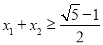 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】“共享单车”的出现,为我们提供了一种新型的交通方式.某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的
 城市和交通拥堵严重的
城市和交通拥堵严重的 城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图(如图所示):
城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图(如图所示):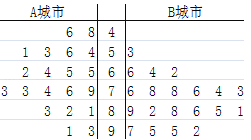
若得分不低于80分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成此
 列联表,并据此样本分析是否有
列联表,并据此样本分析是否有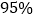 的把握认为城市拥堵与认可共享单车有关:
的把握认为城市拥堵与认可共享单车有关:
合计
认可
不认可
合计
附:参考数据:(参考公式:
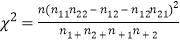 )
)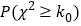
0.150
0.100
0.050
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
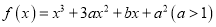 在
在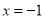 处的极值为0.
处的极值为0.(1)求常数
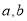 的值;
的值;(2)求
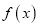 的单调区间;
的单调区间;(3)方程
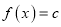 在区间
在区间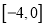 上有三个不同的实根时,求实数
上有三个不同的实根时,求实数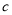 的范围.
的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
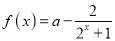 (
(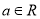 ).
).(1)是否存在实数
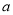 使函数
使函数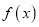 是奇函数?并说明理由;
是奇函数?并说明理由;(2)在(1)的条件下,当
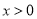 时,
时, 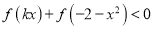 恒成立,求实数
恒成立,求实数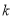 的取值范围.
的取值范围.
相关试题

