【题目】已知数列{an},其前n项和为Sn .
(1)若{an}是公差为d(d>0)的等差数列,且{ ![]() }也为公差为d的等差数列,求数列{an}的通项公式;
}也为公差为d的等差数列,求数列{an}的通项公式;
(2)若数列{an}对任意m,n∈N* , 且m≠n,都有 ![]() =am+an+
=am+an+ ![]() ,求证:数列{an}是等差数列.
,求证:数列{an}是等差数列.
参考答案:
【答案】
(1)解:根据题意得:an=a1+(n﹣1)d,Sn=na1+ ![]() d,
d,
∴ ![]() =
= ![]() 成等差数列,公差为d,
成等差数列,公差为d,
∴ ![]() =dn,
=dn,
∴  ,
,
解得:d= ![]() ,a1=﹣
,a1=﹣ ![]() ,
,
则an= ![]() n﹣
n﹣ ![]()
(2)解:令m=2,n=1,则 ![]() =2a2,即
=2a2,即 ![]() =a2,
=a2,
整理得:a1+a3=2a2,即a1,a2,a3成等差数列,
下面用数学归纳法证明{an}成等差数列,
假设a1,a2,…,ak成等差数列,其中k≥3,公差为d,
则令m=k,n=1, ![]() =ak+a1+d,
=ak+a1+d,
∴2Sk+1=(k+1)(ak+a1+d)=k(ak+a1)+a1+ak+(k+1)d=2Sk+a1+ak+(k+1)d,
∴2ak+1=a1+ak+(k+1)d=2(a1+kd),即ak+1=a1+kd,
∴a1,a2,…,ak,ak+1成等差数列,
则对于一切自然数,数列{an}是等差数列
【解析】(1)利用等差数列的通项公式及前n项和公式表示出an与Sn , 代入验证即可确定出数列{an}的通项公式;(2)令m=2,n=1确定出a1 , a2 , a3成等差数列,再利用数学归纳法证明对于一切n≥3的自然数,数列{an}是等差数列即可.
【考点精析】认真审题,首先需要了解等差关系的确定(如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列),还要掌握等差数列的性质(在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列)的相关知识才是答题的关键.
)那么这个数列就叫做等差数列),还要掌握等差数列的性质(在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公园准备在一圆形水池里设置两个观景喷泉,观景喷泉的示意图如图所示,A,B两点为喷泉,圆心O为AB的中点,其中OA=OB=a米,半径OC=10米,市民可位于水池边缘任意一点C处观赏.

(1)若当∠OBC= 时,sin∠BCO=
时,sin∠BCO=  ,求此时a的值;
,求此时a的值;
(2)设y=CA2+CB2 , 且CA2+CB2≤232.
(i)试将y表示为a的函数,并求出a的取值范围;
(ii)若同时要求市民在水池边缘任意一点C处观赏喷泉时,观赏角度∠ACB的最大值不小于 ,试求A,B两处喷泉间距离的最小值.
,试求A,B两处喷泉间距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为  ,椭圆C 与y 轴交于A,B 两点,且|AB|=2.
,椭圆C 与y 轴交于A,B 两点,且|AB|=2.
(Ⅰ)求椭圆C 的方程;
(Ⅱ)设点P是椭圆C上的一个动点,且点P在y轴的右侧.直线PA,PB与直线x=4分别交于M,N两点.若以MN为直径的圆与x 轴交于两点E,F,求点P横坐标的取值范围及|EF|的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 (a>b>0)的一个顶点为A(2,0),离心率为
(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.(1)求椭圆C的方程;
(2)当△AMN的面积为
 时,求k的值.
时,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ,直线y=
,直线y=  x为曲线y=f(x)的切线(e为自然对数的底数).
x为曲线y=f(x)的切线(e为自然对数的底数).
(1)求实数a的值;
(2)用min{m,n}表示m,n中的最小值,设函数g(x)=min{f(x),x﹣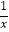 }(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
}(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修:4﹣2:矩阵与变换
若圆C:x2+y2=1在矩阵 (a>0,b>0)对应的变换下变成椭圆E:
(a>0,b>0)对应的变换下变成椭圆E:  ,求矩阵A的逆矩阵A﹣1 .
,求矩阵A的逆矩阵A﹣1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C的极坐标方程是ρ=2sinθ,直线l的参数方程是
 (t为参数).设直线l与x轴的交点是M,N是曲线C上一动点,求MN的最大值.
(t为参数).设直线l与x轴的交点是M,N是曲线C上一动点,求MN的最大值.
相关试题

