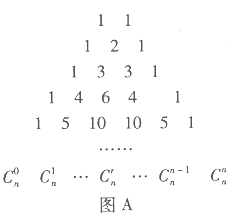
【题目】在我国南宋数学家杨辉所著的《详解九章算法》(1261年)一书中,用如图![]() 所示的三角形,解释二项和的乘方规律.在欧洲直到1623年以后,法国数学家布莱士帕斯卡的著作(1655年)介绍了这个三角形,近年来,国外也逐渐承认这项成果属于中国,所以有些书上称这是“中国三角形”
所示的三角形,解释二项和的乘方规律.在欧洲直到1623年以后,法国数学家布莱士帕斯卡的著作(1655年)介绍了这个三角形,近年来,国外也逐渐承认这项成果属于中国,所以有些书上称这是“中国三角形”![]() ,如图
,如图![]() .17世纪德国数学家莱布尼茨发现了“莱布尼茨三角形”,如图
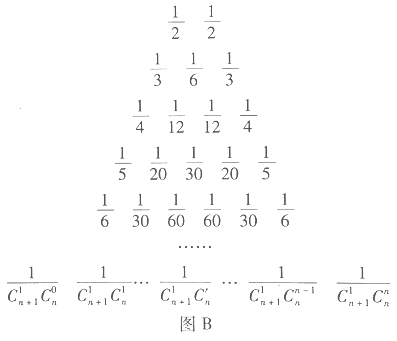
.17世纪德国数学家莱布尼茨发现了“莱布尼茨三角形”,如图![]() .在杨辉三角中,相邻两行满足关系式:
.在杨辉三角中,相邻两行满足关系式:![]() ,其 中
,其 中![]() 是行数,
是行数,![]() .请类比上式,在莱布尼茨三角形中相邻两行满足的关系式是__________.
.请类比上式,在莱布尼茨三角形中相邻两行满足的关系式是__________.
参考答案:
【答案】![]()
【解析】分析:这是一个考查类比推理的题目,解题的关键是仔细观察图中给出的莱布尼茨三角形,并从三解数阵中,找出行与行之间数的关系,探究规律并其表示出来.
详解:类比观察得,将莱布尼茨三角形的每一行都能提出倍数![]() ,
,
而相邻两项之和是上一行的两者相拱之数,所以类比式子![]() ,有
,有![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面几种推理过程是演绎推理的是( )
A. 在数列|
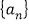 中,
中,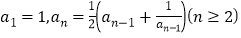 由此归纳出
由此归纳出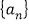 的通项公式
的通项公式B. 由平面三角形的性质,推测空间四面体性质
C. 某校高二共有10个班,1班有51人,2班有53人,3班有52人,由此推测各班都超过50人
D. 两条直线平行,同旁内角互补,如果
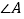 和
和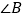 是两条平行直线的同旁内角,则
是两条平行直线的同旁内角,则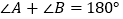
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义方程
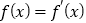 的实数根
的实数根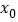 叫做函数
叫做函数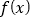 的“新驻点”,若函数
的“新驻点”,若函数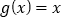 ,
,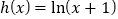 ,
, 的“新驻点”分别为
的“新驻点”分别为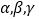 ,则
,则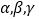 的大小关系为( )
的大小关系为( )A.
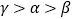 B.
B. 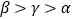 C.
C. 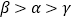 D.
D. 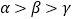
-
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
 的左焦点为F,直线x=m与椭圆相交于点A、B,当△FAB的周长最大时,△FAB的面积是 .
的左焦点为F,直线x=m与椭圆相交于点A、B,当△FAB的周长最大时,△FAB的面积是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】请你帮忙设计2010年玉树地震灾区小学的新校舍,如图,在学校的东北力有一块地,其中两面是不能动的围墙,在边界
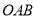 内是不能动的一些体育设施.现准备在此建一栋教学楼,使楼的底面为一矩形,且靠围墙的方向须留有5米宽的空地,问如何设计,才能使教学楼的面积最大?
内是不能动的一些体育设施.现准备在此建一栋教学楼,使楼的底面为一矩形,且靠围墙的方向须留有5米宽的空地,问如何设计,才能使教学楼的面积最大?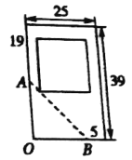
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中
①若
 ,则函数
,则函数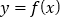 在
在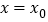 取得极值;
取得极值;②直线
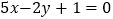 与函数
与函数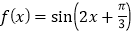 的图像不相切;
的图像不相切;③若
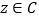 (
(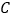 为复数集),且
为复数集),且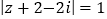 ,则
,则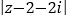 的最小值是3;
的最小值是3;④定积分
 .
.正确的有__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查我市在校中学生参加体育运动的情况,从中随机抽取了16名男同学和14 名女同学,调查发现,男、女同学中分别有12人和6人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下
 列联表:
列联表: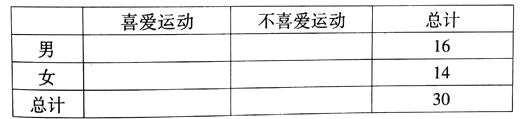
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.010的前提下认为性别与喜爱运动有关?
(3)将以上统计结果中的频率视作概率,从我市中学生中随机抽取3人,若其中喜爱运动的人数为
 ,求
,求 的分布列和均值.
的分布列和均值.参考数据:

相关试题

