【题目】已知函数![]() 。
。
(Ⅰ)当a=2,求函数f(x)的图象在点(1,f(1) )处的切线方程;
(Ⅱ)当a>0时,求函数f(x)的单调区间。
参考答案:
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】【试题分析】(1)先求当![]() 时,函数
时,函数![]() 的导数,求出切线的斜率,再运用直线的点斜式方程求出切线的方程;(2)先对含参数的函数解析式
的导数,求出切线的斜率,再运用直线的点斜式方程求出切线的方程;(2)先对含参数的函数解析式![]() 进行求导,再运用分类整合的数学思想,对实数
进行求导,再运用分类整合的数学思想,对实数![]() 进行分类讨论函数的单调性,分别求出其单调区间:
进行分类讨论函数的单调性,分别求出其单调区间:
(1)当![]() 时,
时, ![]() ,
,
![]() ,
,
![]() 函数
函数![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() .
.
(2)由题知,函数![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
令![]() ,解得
,解得![]() ,
,
(I) 当![]() 时,所以
时,所以![]() ,在区间
,在区间![]() 和
和![]() 上
上![]() ;在区间
;在区间![]() 上
上![]() ,故函数
,故函数![]() 的单调递增区间是
的单调递增区间是![]() 和
和![]() ,单调递减区间是
,单调递减区间是![]() .-
.-
(II)当a=2时,f’(x)>=0 恒成立,故函数f(x)的单调递增区间是(0,+∞)
(III)当1<a<2时,a-1<1,在区间(0,a-1),和(1,+∞)上f’(x)>0 ;在(a-1,1)上f’(x)<0 ,故函数![]() 的单调递增区间是(0,a-1),(1,+∞),单调递减区间是(a-1,1)
的单调递增区间是(0,a-1),(1,+∞),单调递减区间是(a-1,1)
(IV)当a=1时,f’(x)=x-1, x>1时f’(x)>0, x<1时f’(x)<0,
函数![]() 的单调递增区间是 (1,+∞), 单调递减区间是
的单调递增区间是 (1,+∞), 单调递减区间是![]()
(V)当0<a<1时,a-1<0,函数![]() 的单调递增区间是 (1,+∞),
的单调递增区间是 (1,+∞),
单调递减区间是![]() ,
,
综上,(I)![]() 时函数
时函数![]() 的单调递增区间是
的单调递增区间是![]() 和
和![]() ,单调递减区间是
,单调递减区间是![]()
(II) a=2时,函数f(x)的单调递增区间是(0,+∞)-
(III) 当0<a<2时,函数![]() 的单调递增区间是(0,a-1),(1,+∞),单调递减区间是(a-1,1)
的单调递增区间是(0,a-1),(1,+∞),单调递减区间是(a-1,1)
(IV)当0<a≤1时,函数![]() 的单调递增区间是 (1,+∞), 单调递减区间是
的单调递增区间是 (1,+∞), 单调递减区间是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体ABCD-A1B1C1D1中,E,F,P,Q,M,N分别是棱AB,AD,DD1,BB1,A1B1,A1D1的中点.求证:
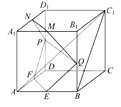
(1)直线BC1∥平面EFPQ.
(2)直线AC1⊥平面PQMN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
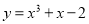 在点
在点 处的切线
处的切线 平行直线
平行直线 ,且点
,且点 在第三象限.
在第三象限.(1)求
 的坐标;
的坐标;(2)若直线
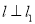 , 且
, 且 也过切点
也过切点 ,求直线
,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
①点P(-1,4)到直线3x+4y =2的距离为3.
②过点M(-3,5)且在两坐标轴上的截距互为相反数的直线方程为
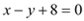 .
.③命题“x∈R,使得x2﹣2x+1<0”的否定是真命题;
④“x ≤1,且y≤1”是“x + y ≤2”的充要条件.
其中不正确命题的序号是 _______________ .(把你认为不正确命题的序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 为奇函数,且x=-1处取得极大 值2.
为奇函数,且x=-1处取得极大 值2.(1)求f(x)的解析式;
(2)过点A(1,t)
 可作函数f(x)图像的三条切线,求实数t的取值范围;
可作函数f(x)图像的三条切线,求实数t的取值范围;(3)若
 对于任意的
对于任意的 恒成立,求实数m取值范围.
恒成立,求实数m取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD .

(1)求证:CD⊥平面ABD;
(2)若AB=BD=CD=1,M为AD中点,求三棱锥A-MBC的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn-an}为等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
相关试题

