【题目】已知函数![]() .
.
(1)当![]() 时,求该函数的定义域;
时,求该函数的定义域;
(2)当![]() 时,如果
时,如果![]() 对任何
对任何![]() 都成立,求实数
都成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,将函数
,将函数![]() 的图像沿
的图像沿![]() 轴方向平移,得到一个偶函数
轴方向平移,得到一个偶函数![]() 的图像,设函数
的图像,设函数![]() 的最大值为
的最大值为![]() ,求
,求![]() 的最小值.
的最小值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)最小值为1.
;(3)最小值为1.
【解析】
(1)解真数大于0的不等式即可;
(2)通过分离参数,将问题转化为恒成立问题,进而求得a的取值范围;
(3)先设出平移t个单位,再根据g(x)为偶函数得![]() ,然后根据对数函数的单调性求得h(a),最后由基本不等式求得h(a)的最小值。
,然后根据对数函数的单调性求得h(a),最后由基本不等式求得h(a)的最小值。
(1)a=-1时,f(x)=log2(ax2+2x-a)=log2(-x2+2x+1),
解-x2+2x+1>0得
![]()
所以函数的定义域为![]()
(2) 当a≤0时,f(x)≥1即log2(ax2+2x-a)≥1,
即ax2+2x-a-2≥0对任何x∈[2,3]都成立,
则 ![]()
令![]() ,因为当x∈[2,3]时
,因为当x∈[2,3]时![]() 是单调递增函数
是单调递增函数
所以![]()
所以![]() ,又因为
,又因为![]()
所以a的取值范围为![]()
(3)当a<0时,设将f(x)的图象沿x轴方向平移t个单位得到g(x)的图象,
则g(x)=![]() [a(x+t)2+2(x+t)-a]=
[a(x+t)2+2(x+t)-a]=![]() [ax2+(2at+2)x+at2+2t-a],
[ax2+(2at+2)x+at2+2t-a],
因为g(x)为偶函数,所以g(-x)=g(x),
则![]() [ax2-(2at+2)x+at2+2t-a]=
[ax2-(2at+2)x+at2+2t-a]=![]() [ax2+(2at+2)x+at2+2t-a],
[ax2+(2at+2)x+at2+2t-a],
所以2at+2=0,所以![]()
所以![]()
因为a<0所以x=0时,![]()
因为![]() 此时
此时![]() ,解得
,解得![]()
所以![]()
即![]() 的最小值为1
的最小值为1
-
科目: 来源: 题型:
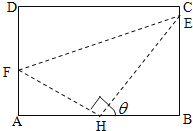
查看答案和解析>>【题目】如图,某污水处理厂要在一个矩形污水处理池
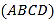 的池底水平铺设污水净化管道(
的池底水平铺设污水净化管道(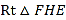 ,
,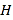 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口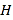 是
是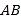 的中点,
的中点,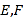 分别落在线段
分别落在线段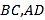 上.已知
上.已知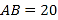 米,
米,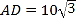 米,记
米,记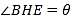 .
.
(1)试将污水净化管道的长度
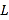 表示为
表示为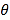 的函数,并写出定义域;
的函数,并写出定义域;(2)若
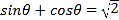 ,求此时管道的长度
,求此时管道的长度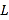 ;
;(3)当
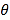 取何值时,污水净化效果最好?并求出此时管道的长度.
取何值时,污水净化效果最好?并求出此时管道的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}满足:a1=2,且a1 , a2 , a5成等比数列.
(1)求数列{an}的通项公式;
(2)记Sn为数列{an}的前n项和,是否存在正整数n,使得Sn>60n+800?若存在,求n的最小值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某轮船公司的一艘轮船每小时花费的燃料费与轮船航行速度的平方成正比,比例系数为
 轮船的最大速度为15海里
轮船的最大速度为15海里 小时
小时 当船速为10海里
当船速为10海里 小时,它的燃料费是每小时96元,其余航行运作费用(不论速度如何)总计是每小时150元
小时,它的燃料费是每小时96元,其余航行运作费用(不论速度如何)总计是每小时150元 假定运行过程中轮船以速度v匀速航行.
假定运行过程中轮船以速度v匀速航行. 求k的值;
求k的值; 求该轮船航行100海里的总费用
求该轮船航行100海里的总费用 燃料费
燃料费 航行运作费用
航行运作费用 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的命题的序号为__________.
①已知随机变量服从二项分布
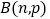 ,若
,若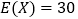 ,
,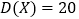 ,则
,则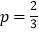 ;
;②将一组数据中的每个数据都加上同一个常数后,方差恒不变;
③设随机变量
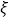 服从正态分布
服从正态分布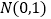 ,若
,若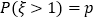 ,则
,则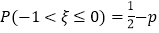 ;
;④某人在
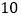 次射击中,击中目标的次数为
次射击中,击中目标的次数为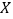 ,
,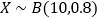 ,则当
,则当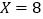 时概率最大.
时概率最大. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
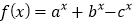 ,其中
,其中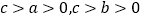 ,若
,若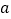 、
、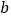 、
、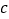 是
是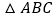 的三条边长,则下列结论:①对于一切
的三条边长,则下列结论:①对于一切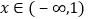 都有
都有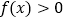 ;②存在
;②存在 使
使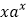 、
、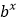 、
、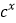 不能构成一个三角形的三边长;③
不能构成一个三角形的三边长;③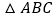 为钝角三角形,存在
为钝角三角形,存在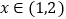 ,使
,使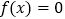 ,其中正确的个数为______个
,其中正确的个数为______个A. 3B. 2C. 1D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是定义在
是定义在 上的函数,如果存在常数
上的函数,如果存在常数 ,对区间
,对区间 的任意划分:
的任意划分: ,和式
,和式 恒成立,则称
恒成立,则称 为
为 上的“绝对差有界函数”,注:
上的“绝对差有界函数”,注: .
.(1)求证:函数
 在
在 上是“绝对差有界函数”;
上是“绝对差有界函数”;(2)记集合
 存在常数
存在常数 ,对任意的
,对任意的 ,有
,有 成立.
成立.求证:集合
 中的任意函数
中的任意函数 为“绝对差有界函数”;
为“绝对差有界函数”;(3)求证:函数
 不是
不是 上的“绝对差有界函数”.
上的“绝对差有界函数”.
相关试题

