【题目】某校的一个社会实践调查小组,在对该校学生的良好“用眼习惯”的调查中,随机发放了120分问卷.对收回的100份有效问卷进行统计,得到如![]() 下列联表:
下列联表:
做不到科学用眼 | 能做到科学用眼 | 合计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
(1)现按女生是否能做到科学用眼进行分层,从45份女生问卷中抽取了6份问卷,从这6份问卷中再随机抽取3份,并记其中能做到科学用眼的问卷的份数![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若在犯错误的概率不超过![]() 的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的
的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量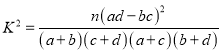 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
参考答案:
【答案】(1)分布列见解析, ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)分层从![]() 份女生问卷中抽取了
份女生问卷中抽取了![]() 份问卷,其中“科学用眼”抽
份问卷,其中“科学用眼”抽![]() 人,“不科学用眼”抽
人,“不科学用眼”抽![]() 人,若从这
人,若从这![]() 份问卷中随机抽取
份问卷中随机抽取![]() 份,随机变量
份,随机变量![]() .利用“超几何分布”即可得出分布列及其数学期望;(2)根据“独立性检验的基本思想的应用”计算公式可得
.利用“超几何分布”即可得出分布列及其数学期望;(2)根据“独立性检验的基本思想的应用”计算公式可得![]() 的观测值
的观测值![]() ,即可得出.
,即可得出.
试题解析:(1)“科学用眼”抽![]() 人,“不科学用眼”抽
人,“不科学用眼”抽![]() 人.
人.
则随机变量![]() ,
,
∴![]() ,
,![]() ,
,![]()
分布列为
| 0 | 1 | 2 |
|
|
|
|
![]()
(2)![]()
由表可知2.706<3.030<3.840;
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】4月16日摩拜单车进驻大连市旅顺口区,绿色出行引领时尚,旅顺口区对市民进行“经常使用共享单车与年龄关系”的调查统计,若将单车用户按照年龄分为“年轻人”(20岁~39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类,抽取一个容量为200的样本,将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”。使用次数为5次或不足5次的称为“不常使用单车用户”,已知“经常使用单车用户”有120人,其中
 是“年轻人”,已知“不常使用单车用户”中有
是“年轻人”,已知“不常使用单车用户”中有 是“年轻人”.
是“年轻人”.(1)请你根据已知的数据,填写下列
 列联表:
列联表:年轻人
非年轻人
合计
经常使用单车用户
不常使用单车用户
合计
(2)请根据(1)中的列联表,计算
 值并判断能否有
值并判断能否有 的把握认为经常使用共享单车与年龄有关?
的把握认为经常使用共享单车与年龄有关?(附:

当
 时,有
时,有 的把握说事件
的把握说事件 与
与 有关;当
有关;当 时,有
时,有 的把握说事件
的把握说事件 与
与 有关;当
有关;当 时,认为事件
时,认为事件 与
与 是无关的)
是无关的) -
科目: 来源: 题型:
查看答案和解析>>【题目】在
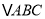 中,
中, 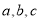 分别是角
分别是角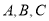 的对边,且
的对边,且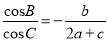 ,若
,若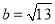 ,
, 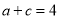 ,则
,则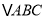 的面积为( )
的面积为( )A.
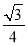 B.
B. 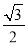 C.
C. 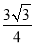 D.
D. 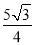
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了纪念“中国红军长征90周年”,增强学生对“长征精神”的深刻理解,在全校组织了一次有关“长征”的知识竞赛,经过初赛、复赛,甲、乙两个代表队(每队3人)进入了决赛,规定每人回答一个问题,答对为本队赢得20分,答错得0分.假设甲队中每人答对的概率均为
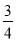 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为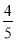 ,
, 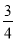 ,
, 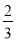 ,且各人回答正确与否相互之间没有影响,用
,且各人回答正确与否相互之间没有影响,用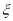 表示乙队的总得分.
表示乙队的总得分.(1)求
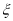 的分布列和均值;
的分布列和均值;(2)求甲、乙两队总得分之和等于40分且甲队获胜的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
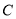 的极坐标方程为
的极坐标方程为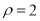 ,在以极点为直角坐标原点
,在以极点为直角坐标原点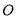 ,极轴为
,极轴为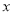 轴的正半轴建立的平面直角坐标系
轴的正半轴建立的平面直角坐标系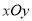 中,直线
中,直线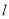 的参数方程为
的参数方程为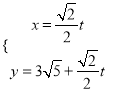 (
(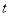 为参数).
为参数).(1)写出直线
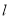 的普通方程与曲线
的普通方程与曲线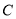 的直角坐标方程;
的直角坐标方程;(2)在平面直角坐标系中,设曲线
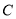 经过伸缩变换
经过伸缩变换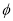 :
:  得到曲线
得到曲线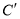 ,若
,若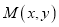 为曲线
为曲线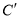 上任意一点,求点
上任意一点,求点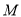 到直线
到直线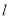 的最小距离.
的最小距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
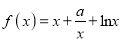 ,(
,( 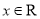 ).
).(Ⅰ)若
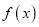 有最值,求实数
有最值,求实数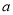 的取值范围;
的取值范围;(Ⅱ)当
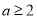 时,若存在
时,若存在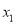 、
、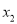 (
(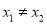 ),使得曲线
),使得曲线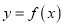 在
在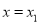 与
与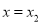 处的切线互相平行,求证:
处的切线互相平行,求证: 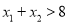 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者
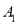 ,
, 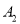 ,
, 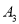 ,
,  ,
, 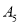 ,
, 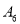 和4名
和4名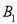 ,
, 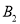 ,
, 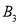 ,
, 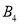 ,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.
,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.(Ⅰ)求接受甲种心理暗示的志愿者中包含
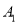 但不包含
但不包含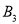 的频率.
的频率.(Ⅱ)用
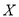 表示接受乙种心理暗示的女志愿者人数,求
表示接受乙种心理暗示的女志愿者人数,求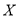 的分布列与数学期望
的分布列与数学期望 .
.
相关试题

