【题目】某校为了纪念“中国红军长征90周年”,增强学生对“长征精神”的深刻理解,在全校组织了一次有关“长征”的知识竞赛,经过初赛、复赛,甲、乙两个代表队(每队3人)进入了决赛,规定每人回答一个问题,答对为本队赢得20分,答错得0分.假设甲队中每人答对的概率均为![]() ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为![]() ,
, ![]() ,
, ![]() ,且各人回答正确与否相互之间没有影响,用
,且各人回答正确与否相互之间没有影响,用![]() 表示乙队的总得分.
表示乙队的总得分.
(1)求![]() 的分布列和均值;
的分布列和均值;
(2)求甲、乙两队总得分之和等于40分且甲队获胜的概率.
参考答案:
【答案】(1) ![]() 的分布列为:
的分布列为:
| 0 | 20 | 40 | 60 |
|
|
|
|
|
![]() .
.
;(2) ![]() .
.
【解析】试题分析:(1)明确![]() 的所有可能取值,并确定相应的概率,从而得到分布列及期望;(2)记“甲队得40分,乙队得0分”为事件
的所有可能取值,并确定相应的概率,从而得到分布列及期望;(2)记“甲队得40分,乙队得0分”为事件![]() ,则
,则![]() 。
。
试题解析:
(1)由题意知, ![]() 的所有可能取值为0,20,40,60.
的所有可能取值为0,20,40,60.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 的分布列为:
的分布列为:
| 0 | 20 | 40 | 60 |
|
|
|
|
|
所以![]() .
.
(2)记“甲队得40分,乙队得0分”为事件![]() .
.
又![]() ,
,
故甲、乙两队总得分之和为40分且甲队获胜的概率为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
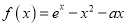 .
.(1)
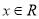 时,证明:
时,证明: 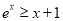 ;
;(2)当
 时,直线
时,直线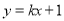 和曲线
和曲线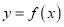 切于点
切于点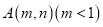 ,求实数
,求实数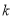 的值;
的值;(3)当
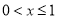 时,不等式
时,不等式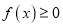 恒成立,求实数
恒成立,求实数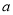 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】4月16日摩拜单车进驻大连市旅顺口区,绿色出行引领时尚,旅顺口区对市民进行“经常使用共享单车与年龄关系”的调查统计,若将单车用户按照年龄分为“年轻人”(20岁~39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类,抽取一个容量为200的样本,将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”。使用次数为5次或不足5次的称为“不常使用单车用户”,已知“经常使用单车用户”有120人,其中
 是“年轻人”,已知“不常使用单车用户”中有
是“年轻人”,已知“不常使用单车用户”中有 是“年轻人”.
是“年轻人”.(1)请你根据已知的数据,填写下列
 列联表:
列联表:年轻人
非年轻人
合计
经常使用单车用户
不常使用单车用户
合计
(2)请根据(1)中的列联表,计算
 值并判断能否有
值并判断能否有 的把握认为经常使用共享单车与年龄有关?
的把握认为经常使用共享单车与年龄有关?(附:

当
 时,有
时,有 的把握说事件
的把握说事件 与
与 有关;当
有关;当 时,有
时,有 的把握说事件
的把握说事件 与
与 有关;当
有关;当 时,认为事件
时,认为事件 与
与 是无关的)
是无关的) -
科目: 来源: 题型:
查看答案和解析>>【题目】在
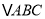 中,
中, 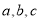 分别是角
分别是角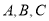 的对边,且
的对边,且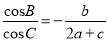 ,若
,若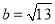 ,
, 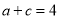 ,则
,则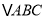 的面积为( )
的面积为( )A.
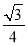 B.
B. 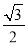 C.
C. 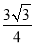 D.
D. 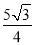
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校的一个社会实践调查小组,在对该校学生的良好“用眼习惯”的调查中,随机发放了120分问卷.对收回的100份有效问卷进行统计,得到如
 下列联表:
下列联表:做不到科学用眼
能做到科学用眼
合计
男
45
10
55
女
30
15
45
合计
75
25
100
(1)现按女生是否能做到科学用眼进行分层,从45份女生问卷中抽取了6份问卷,从这6份问卷中再随机抽取3份,并记其中能做到科学用眼的问卷的份数
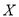 ,试求随机变量
,试求随机变量 的分布列和数学期望;
的分布列和数学期望;(2)若在犯错误的概率不超过
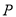 的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的
的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的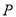 的值应为多少?请说明理由.
的值应为多少?请说明理由.附:独立性检验统计量
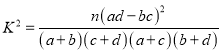 ,其中
,其中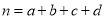 .
.独立性检验临界值表:

0.25
0.15
0.10
0.05
0.025

1.323
2.072
2.706
3.840
5.024
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
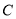 的极坐标方程为
的极坐标方程为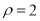 ,在以极点为直角坐标原点
,在以极点为直角坐标原点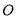 ,极轴为
,极轴为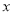 轴的正半轴建立的平面直角坐标系
轴的正半轴建立的平面直角坐标系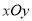 中,直线
中,直线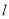 的参数方程为
的参数方程为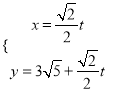 (
(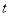 为参数).
为参数).(1)写出直线
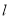 的普通方程与曲线
的普通方程与曲线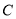 的直角坐标方程;
的直角坐标方程;(2)在平面直角坐标系中,设曲线
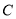 经过伸缩变换
经过伸缩变换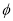 :
:  得到曲线
得到曲线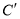 ,若
,若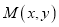 为曲线
为曲线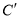 上任意一点,求点
上任意一点,求点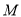 到直线
到直线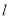 的最小距离.
的最小距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
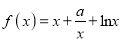 ,(
,( 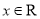 ).
).(Ⅰ)若
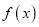 有最值,求实数
有最值,求实数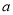 的取值范围;
的取值范围;(Ⅱ)当
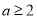 时,若存在
时,若存在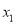 、
、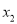 (
(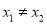 ),使得曲线
),使得曲线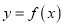 在
在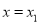 与
与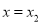 处的切线互相平行,求证:
处的切线互相平行,求证: 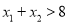 .
.
相关试题

