【题目】已知函数![]() 在
在![]() 处有极值
处有极值![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的单调区间.
的单调区间.
参考答案:
【答案】(1)![]() ;(2)单调减区间是(0,1),单调增区间是(1,+∞).
;(2)单调减区间是(0,1),单调增区间是(1,+∞).
【解析】试题分析: (1)f′(x)=2ax+![]() .由题意可得:
.由题意可得: 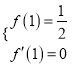 ,解得a,b.
,解得a,b.
(2)f(x)=![]() x2-lnx,f′(x)=x﹣
x2-lnx,f′(x)=x﹣![]() .函数定义域为(0,+∞).令f′(x)>0,f′(x)<0,分别解出即可得出单调区间.
.函数定义域为(0,+∞).令f′(x)>0,f′(x)<0,分别解出即可得出单调区间.
试题解析:
(1)∵f′(x)=2ax+![]() .又f(x)在x=1处有极值
.又f(x)在x=1处有极值![]() ,
,
∴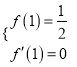 即
即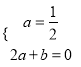 解得a=
解得a=![]() ,b=-1.
,b=-1.
(2)由(1)可知f(x)=![]() x2-lnx,其定义域是(0,+∞),
x2-lnx,其定义域是(0,+∞),
f′(x)=x-![]() =
=![]() .
.
由f′(x)<0,得0<x<1;由f′(x)>0,得x>1.
所以函数y=f(x)的单调减区间是(0,1),单调增区间是(1,+∞).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, (其中
(其中 ,
, ,
, )的图象的两条相邻对称轴之间的距离为
)的图象的两条相邻对称轴之间的距离为 ,且图象上一个最低点为
,且图象上一个最低点为 .
.(1)求函数
 的解析式;
的解析式;(2)当
 时,求函数
时,求函数 的值域;
的值域;(3)若方程
 在
在 上有两个不相等的实数根
上有两个不相等的实数根 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某儿童节在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.记两次记录的数分别为x,y.奖励规则如下:
①若xy≤3,则奖励玩具一个;
②若xy≥8,则奖励水杯一个;
③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀,小亮准备参加此项活动.
(1)求小亮获得玩具的概率;
(2)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 三个顶点坐标分别为:
三个顶点坐标分别为: 直线
直线 经过点
经过点
(1)求
 外接圆
外接圆 的方程.
的方程.(2)若直线
 与
与 相交于
相交于 两点,且
两点,且 ,求直线
,求直线 的方程.
的方程. -
科目: 来源: 题型:
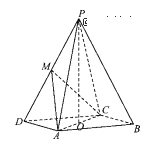
查看答案和解析>>【题目】在四棱锥P-ABC中,底面ABCD为平行四边形,
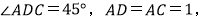 ,O为AC的中点,
,O为AC的中点, 平面
平面 M为PD的中点。
M为PD的中点。(1)证明
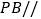 平面
平面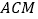 .
.(2)证明
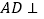 平面
平面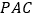 .
.(3)求三棱锥P-MAC体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)=2
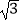 sin(π﹣x)sinx﹣(sinx﹣cosx)2 .
sin(π﹣x)sinx﹣(sinx﹣cosx)2 .
(1)求f(x)的单调递增区间;
(2)把y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移 个单位,得到函数y=g(x)的图象,求g(
个单位,得到函数y=g(x)的图象,求g(  )的值.
)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
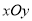 中,直线
中,直线 与抛物线
与抛物线 相交于
相交于 、
、 两点.
两点.(1)求证:“如果直线
 过点
过点 ,那么
,那么 ”是真命题;
”是真命题;(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
相关试题

