【题目】已知正三棱柱![]() 的所有棱长都相等,
的所有棱长都相等,![]() 分别为
分别为![]() 的中点.现有下列四个结论:
的中点.现有下列四个结论:
![]() :
:![]() ;
; ![]() :
:![]() ;
;
![]() :
:![]() 平面
平面![]() ;
; ![]() :异面直线
:异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
其中正确的结论是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】C
【解析】分析:根据题意,判断AC1与MN不平行,是异面直线,知p1错误;利用线面垂直的定义判断A1C⊥C1N,知p2正确;判断B1C⊥平面AOP,得出B1C与平面AMN不垂直,知p3错误;找出异面直线AB与MN所成的角,计算余弦值,知p4正确.
详解:正三棱柱ABC﹣A1B1C1的所有棱长都相等,M,N分别为B1C1,BB1的中点;

对于p1:如图①所示,
MN∥BC1,BC1∩AC1=C1,
∴AC1与MN不平行,是异面直线,p1错误;

对于p2:如图②所示,
连接AC1,交A1C于点O,连接ON,
易知A1C⊥AC1,ON⊥平面ACC1A1,
∴ON⊥A1C,
又ON∩AC1=O,
∴A1C⊥平面ONC1,
∴A1C⊥C1N,p2正确;

对于p3:如图③所示,
取BC的中点O,连接AO,BC1,
过点O作OP∥BC1,交CC1于点P,
连接AP,则AO⊥平面BCC1B1,
∴AO⊥B1C,
又BC1∩⊥OP,
∴B1C⊥OP,
∴B1C⊥平面AOP,
又平面ABC1与平面AOP有公共点A,
∴B1C与平面AMN不垂直,p3错误;

对于p4,如图④所示,
连接BC1,AC1,则MN∥BC1,
∴∠ABC1是异面直线AB与MN所成的角,
设AB=1,则AC1=BC1=![]() ,
,
∴cos∠ABC1=![]() p4正确.
p4正确.
综上,其中正确的结论是p2、p4.
故答案为:C
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=|x+2|﹣|2x﹣1|,M为不等式f(x)>0的解集.
(1)求M;
(2)求证:当x,y∈M时,|x+y+xy|<15. -
科目: 来源: 题型:
查看答案和解析>>【题目】执行如图所示的程序框图,若输出的
 ,则判断框内可以填入
,则判断框内可以填入
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知偶函数
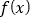 在
在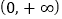 上单调递增,则
上单调递增,则A.
 B.
B. 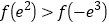
C.
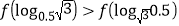 D.
D. 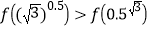
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
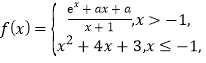 则关于
则关于 的方程
的方程 的实数解最多有
的实数解最多有A. 4个 B. 7个 C. 10个 D. 12个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, ,
, ,
, ,
, ,
, ,点
,点 为
为 的中点.
的中点.
(1)求证:
 平面
平面 ;
;(2)若平面

 平面
平面 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】以下判断正确的是( )
A.函数y=f(x)为R上可导函数,则f'(x0)=0是x0为函数f(x)极值点的充要条件
B.命题“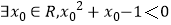 ”的否定是“?x∈R,x2+x﹣1>0”
”的否定是“?x∈R,x2+x﹣1>0”
C.“ ”是“函数f(x)=sin(ωx+φ)是偶函数”的充要条件
”是“函数f(x)=sin(ωx+φ)是偶函数”的充要条件
D.命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题
相关试题

