【题目】如图所示,正方体ABCD-A1B1C1D1中,M、N分别是A1B1、B1C1的中点,问:

(1)AM和CN是否是异面直线?说明理由;
(2)D1B和CC1是否是异面直线?说明理由.
参考答案:
【答案】(1)不是异面直线(2)是异面直线
【解析】试题分析:(1)根据公理4得MN∥A1C1∥AC,所以两直线共面(2)由异面直线判定定理可得两直线为异面直线
试题解析: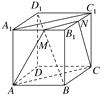
(1)不是异面直线,理由:连结MN,A1C1、AC,如图,因为M、N分别是A1B1、B1C1的中点,所以MN∥A1C1.又因为A1A![]() D1D,D1D
D1D,D1D![]() C1C,所以A1A
C1C,所以A1A![]() C1C,四边形A1ACC1为平行四边形,所以A1C1∥AC,故MN∥A1C1∥AC,所以A、M、N、C在同一个平面内,故AM和CN不是异面直线.
C1C,四边形A1ACC1为平行四边形,所以A1C1∥AC,故MN∥A1C1∥AC,所以A、M、N、C在同一个平面内,故AM和CN不是异面直线.
(2)是异面直线,证明如下:假设D1B与CC1在同一个平面CC1D1内,则B∈平面CC1D1,C∈平面CC1D1,所以BC平面CC1D1,这显然是不正确的,所以假设不成立,故D1B与CC1是异面直线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点,F为AA1的中点.求证:CE,D1F,DA三线交于一点.
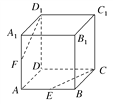
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是__________.(写出所有正确命题的序号)
①已知
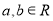 ,“
,“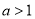 且
且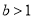 ”是“
”是“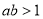 ”的充要条件;
”的充要条件;②已知平面向量
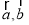 ,“
,“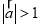 且
且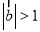 ”是“
”是“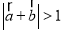 ”的必要不充分条件;
”的必要不充分条件;③已知
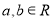 ,“
,“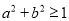 ”是“
”是“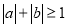 ”的充分不必要条件;
”的充分不必要条件;④命题
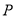 :“
:“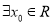 ,使
,使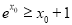 且
且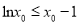 ”的否定为
”的否定为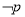 :“
:“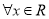 ,都有
,都有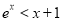 且
且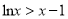 ”
” -
科目: 来源: 题型:
查看答案和解析>>【题目】已知焦点在
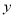 轴上的椭圆
轴上的椭圆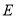 的中心是原点
的中心是原点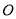 ,离心率为双曲线
,离心率为双曲线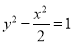 离心率的一半,直线
离心率的一半,直线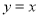 被椭圆
被椭圆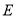 截得的线段长为
截得的线段长为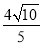 .直线
.直线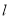 :
: 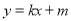 与
与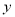 轴交于点
轴交于点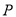 ,与椭圆
,与椭圆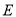 交于
交于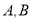 两个相异点,且
两个相异点,且 .
.(1)求椭圆
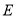 的方程;
的方程;(2)是否存在实数
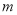 ,使
,使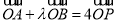 ?若存在,求
?若存在,求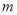 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中,
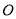 是坐标原点,动圆
是坐标原点,动圆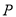 经过点
经过点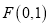 ,且与直线
,且与直线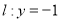 相切.
相切.(1)求动圆圆心
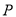 的轨迹方程
的轨迹方程 ;
;(2)过
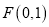 的直线
的直线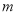 交曲线
交曲线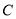 于
于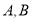 两点,过
两点,过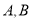 作曲线
作曲线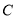 的切线
的切线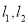 ,直线
,直线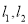 交于点
交于点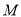 ,求
,求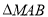 的面积的最小值.
的面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在哈尔滨的中央大街的步行街同侧有6块广告牌,牌的底色可选用红、蓝两种颜色,若要求相邻两块牌的底色不都为蓝色,则不同的配色方案共有( )
A. 20 B. 21 C. 22 D. 24
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
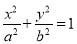 (
( )的离心率为
)的离心率为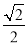 ,短轴的一个端点为
,短轴的一个端点为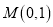 .过椭圆左顶点
.过椭圆左顶点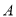 的直线
的直线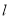 与椭圆的另一交点为
与椭圆的另一交点为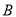 .
.(1)求椭圆的方程;
(2)若
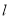 与直线
与直线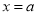 交于点
交于点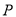 ,求
,求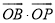 的值;
的值;(3)若
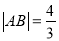 ,求直线
,求直线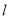 的倾斜角.
的倾斜角.
相关试题

