【题目】2名女生、4名男生排成一排,求:
(1)2名女生不相邻的不同排法共有多少种?
(2)女生甲必须排在女生乙的左边(不一定相邻)的不同排法共有多少种?
参考答案:
【答案】(1)480种(2)360种
【解析】
(1)不相邻问题利用插空法法;
(2)女生顺序已定,先排女生,再排男生,最后根据分步乘法计算原理计算可得;
解:(1)2名女生不相邻的排列可以分成2步完成:
第一步 将4名男生排成一排,有![]() 种排法;
种排法;
第二步 排2名女生.由于2名女生不相邻,可以在每2名男生之间及两端共5个位置中选出2个排2名女生,有![]() 种排法.
种排法.
根据分步计数原理,不同的排法种数是![]() .
.
(2)女生甲必须排在女生乙左边的排列可以分成2步完成:
第一步:排2名女生,女生的顺序已经确定,这2名女生的排法种数为从6个位置中选出2个位置的组合数,即为![]() ;
;
第二步:排4名男生.将4名男生在剩下的4个位置上进行排列的方法数有![]() 种.
种.
根据分步计数原理,不同的排法种数是![]() .
.
答:分别有480和360种不同的排法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|y=ln(﹣x2﹣x+12)},B={x|m﹣1<x<2m+1,m∈R}.
(1)若m=2,求(RA)∩B;
(2)若A∩B=B,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样的方法从该地区调查了500位老年人,结果如下:
性别
是否需要志愿者
男
女
需要
40
30
不需要
160
270
附:
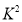 的观测值
的观测值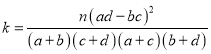
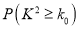
0.05
0.01
0.001
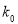
3.841
6.635
10.828
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)在犯错误的概率不超过0.01的前提下是否可认为该地区的老年人是否需要志愿者提供帮助与性别有关?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知角α的顶点与原点O重合,始边与x轴的非负半轴重合,它的终边上有一点P的坐标是(3a,a),其中a≠0.
(1)求cos(α
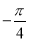 )的值;
)的值;(2)若tan(2α+β)=1,求tanβ的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
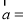 (2sinx,cosx),
(2sinx,cosx),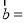 (
(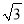 cosx,2cosx).
cosx,2cosx).(1)若x≠kπ
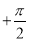 ,k∈Z,且
,k∈Z,且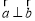 ,求2sin2x﹣cos2x的值;
,求2sin2x﹣cos2x的值;(2)定义函数f(x)
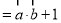 ,求函数f(x)的单调递减区间;并求当x∈[0,
,求函数f(x)的单调递减区间;并求当x∈[0,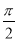 ]时,函数f(x)的值域.
]时,函数f(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
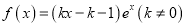 .
.(1)求函数
 的极值;
的极值;(2)求函数
 在区间
在区间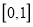 上的最大值
上的最大值 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在底面边长为
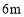 、高为
、高为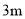 的正六棱柱
的正六棱柱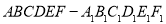 展厅内,长为
展厅内,长为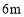 ,宽为
,宽为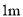 的矩形油画
的矩形油画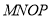 挂在厅内正前方中间.
挂在厅内正前方中间.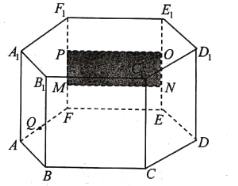
(1)求证:平面
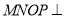 平面
平面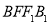 ;
;(2)当游客
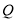 在
在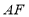 上看油画的纵向视角(即
上看油画的纵向视角(即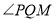 )最大时,求
)最大时,求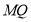 与油画平面所成的角.
与油画平面所成的角.
相关试题

