搜索
【题目】已知函数
.
（1）求函数
的极值；
（2）求函数在区间
上的最大值
.
参考答案：
【答案】（1）见解析（2）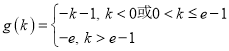
【解析】
（1）首先求出函数的导函数，令
解得
，再对
分类讨论即可得解；
（2）对分类讨论，结合（1）中的结论，计算可得；
解：（1）因为
，所以
，
由解得.
①当
时，
|
|
|
|
| - | 0 | + |
|
| 极小值 |
|
所以，当时，
有极小值
；
②当
时，
|
|
|
|
| + | 0 | - |
|
| 极大值 |
|
所以，当时，有极大值；
综上，当时，当时，有极小值；
当时，当时，有极大值.
（2）当时，由（1）知，为
上单调减函数，而
，
所以，为
上单调减函数，故的最大值
；
当
时，
，由（1）知，为
上单调减函数，而
，
所以，为上单调减函数，故的最大值；
当
时，由（1）知，为
上单调减函数，
上单调增函数，
又满足
，故的最大值；
当
时，由（1）知，为上单调减函数，上单调增函数，
又满足
，故的最大值
；
综上，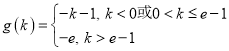
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，已知角α的顶点与原点O重合，始边与x轴的非负半轴重合，它的终边上有一点P的坐标是（3a，a），其中a≠0．
（1）求cos（α
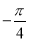）的值；（2）若tan（2α+β）＝1，求tanβ的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】2名女生、4名男生排成一排，求：
（1）2名女生不相邻的不同排法共有多少种？
（2）女生甲必须排在女生乙的左边（不一定相邻）的不同排法共有多少种？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知向量
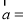（2sinx，cosx），
（
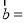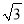cosx，2cosx）．（1）若x≠kπ
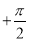，k∈Z，且
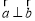，求2sin2x﹣cos2x的值；（2）定义函数f（x）
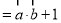，求函数f（x）的单调递减区间；并求当x∈[0，
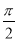]时，函数f（x）的值域． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在底面边长为
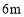、高为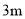
的正六棱柱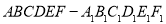
展厅内，长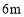为，宽为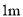
的矩形油画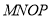
挂在厅内正前方中间.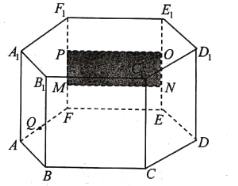
（1）求证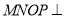：平面
平面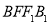
；（2）当游客
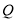在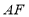
上看油画的纵向视角（即
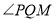）最大时，求
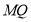与油画平面所成的角. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
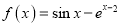，求证：（1）
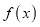在区间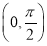
存在唯一极大值点；（2）
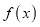在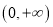
上有且仅有2个零点. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知奇函数f（x）
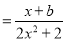，函数g（θ）＝cos2θ+2sinθ
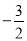，θ∈[m，
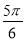]．m，b∈R．（1）求b的值；
（2）判断函数f（x）在[0，1]上的单调性，并证明；
（3）当x∈[0，1]时，函数g（θ）的最小值恰为f（x）的最大值，求m的取值范围．
相关试题
