【题目】已知集合A={x|y=ln(﹣x2﹣x+12)},B={x|m﹣1<x<2m+1,m∈R}.
(1)若m=2,求(RA)∩B;
(2)若A∩B=B,求实数m的取值范围.
参考答案:
【答案】(1){x|3≤x<5};(2)(﹣∞,1]
【解析】
(1)先化简集合A,再求得RA,由m=2,得B={x|1<x<5},然后求(RA)∩B.
(2)由A∩B=B,得到BA,再分B=时,由m﹣1≥2m+1求解,当B≠时,有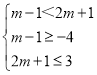 求解,最后取并集.
求解,最后取并集.
(1)集合A={x|y=ln(﹣x2﹣x+12)}={x|﹣x2﹣x+12>0}={x|﹣4<x<3},
所以RA={x|x≤﹣4或x≥3},
当m=2时,B={x|m﹣1<x<2m+1,m∈R}={x|1<x<5},
所以(RA)∩B={x|3≤x<5}.
(2)因为A∩B=B,所以BA,
当B=时,m﹣1≥2m+1,解得m≤﹣2;
当B≠时,有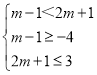 ,解得﹣2<m≤1,
,解得﹣2<m≤1,
综上:实数m的取值范围是(﹣∞,1].
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数y=f(x),若在其定义域内存在x0,使得x0f(x0)=1成立,则称函数f(x)具有性质M.
(1)下列函数中具有性质M的有____
①f(x)=﹣x+2
②f(x)=sinx(x∈[0,2π])
③f(x)=x
 ,(x∈(0,+∞))
,(x∈(0,+∞))④f(x)
(2)若函数f(x)=a(|x﹣2|﹣1)(x∈[﹣1,+∞))具有性质M,则实数a的取值范围是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某媒体为调查喜爱娱乐节目
 是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图: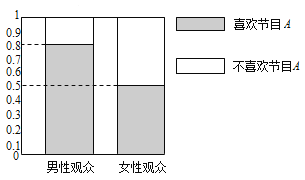
(1)根据该等高条形图,完成下列
 列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目
列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目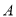 与观众性别有关?
与观众性别有关?
(2)从性观众中按喜欢节目
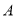 与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目
与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目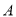 和1名不喜欢节目
和1名不喜欢节目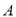 的概率.
的概率.附:
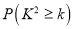
0.100
0.050
0.010
0.001
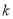
2.706
3.841
6.635
10.828
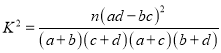 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】西光厂眼镜车间接到一批任务,需要加工6000个
 型零件和2000个
型零件和2000个 型零件.这个车间有214名工人,他们每一个人加工5个
型零件.这个车间有214名工人,他们每一个人加工5个 型零件的时间可以加工3个
型零件的时间可以加工3个 型零件.将这些工人分成两组,两组同时工作,每组加工一种型号的零件,为了在最短的时间内完成这批任务,应怎样分组?
型零件.将这些工人分成两组,两组同时工作,每组加工一种型号的零件,为了在最短的时间内完成这批任务,应怎样分组? -
科目: 来源: 题型:
查看答案和解析>>【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样的方法从该地区调查了500位老年人,结果如下:
性别
是否需要志愿者
男
女
需要
40
30
不需要
160
270
附:
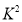 的观测值
的观测值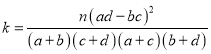
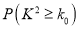
0.05
0.01
0.001
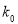
3.841
6.635
10.828
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)在犯错误的概率不超过0.01的前提下是否可认为该地区的老年人是否需要志愿者提供帮助与性别有关?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知角α的顶点与原点O重合,始边与x轴的非负半轴重合,它的终边上有一点P的坐标是(3a,a),其中a≠0.
(1)求cos(α
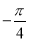 )的值;
)的值;(2)若tan(2α+β)=1,求tanβ的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2名女生、4名男生排成一排,求:
(1)2名女生不相邻的不同排法共有多少种?
(2)女生甲必须排在女生乙的左边(不一定相邻)的不同排法共有多少种?
相关试题

