【题目】某中学调查了某班全部![]() 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 |
|
|
未参加演讲社团 |
|
|
(1)从该班随机选![]() 名同学,求该同学至少参加上述一个社团的概率;
名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的![]() 名同学中,有5名男同学
名同学中,有5名男同学![]()
![]() 名女同学
名女同学![]() 现从这
现从这![]() 名男同学和
名男同学和![]() 名女同学中各随机选
名女同学中各随机选![]() 人,求
人,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由调查数据可知,既未参加书法社团又未参加演讲社团的有![]() 人,故至少参加上述一个社团的共有
人,故至少参加上述一个社团的共有![]() 人,所以从该班级随机选
人,所以从该班级随机选![]() 名同学,该同学至少参加上述一个社团的概率为
名同学,该同学至少参加上述一个社团的概率为![]()
(2)从这![]() 名男同学和
名男同学和![]() 名女同学中各随机选
名女同学中各随机选![]() 人,其一切可能的结果组成的基本事件有:
人,其一切可能的结果组成的基本事件有:![]()
![]() ,共
,共![]() 个.
个.
根据题意,这些基本事件的出现是等可能的.
事件“![]() 被选中且
被选中且![]() 未被选中”所包含的基本事件有:
未被选中”所包含的基本事件有:![]() ,共
,共![]() 个.
个.
因此![]() 被选中且
被选中且![]() 未被选中的概率为
未被选中的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】校园准备绿化一块直径为
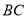 的半圆形空地,点
的半圆形空地,点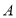 在半圆圆弧上,△
在半圆圆弧上,△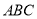 外的地方种草,△
外的地方种草,△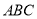 的内接正方形
的内接正方形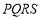 为一水池(
为一水池(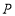 ,
,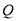 在
在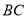 边上),其余地方种花,若
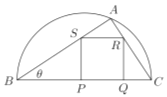
边上),其余地方种花,若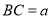 ,
, 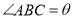 ,设△
,设△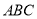 的面积为
的面积为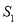 ,正方形面积为
,正方形面积为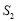 ;
;
(1)用
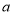 和
和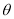 表示
表示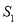 和
和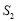 ;
;(2)当
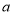 固定,
固定,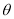 变化时,求
变化时,求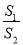 最小值及此时的角
最小值及此时的角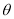 ;
; -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, ;
;(1)若
 ,求函数
,求函数 在
在 上的最大值和最小值;
上的最大值和最小值;(2)若函数
 在
在 上既无最大值又无最小值,求角
上既无最大值又无最小值,求角 的范围;
的范围;(3)若函数
 在
在 上有最小值
上有最小值 ,求
,求 的值;
的值; -
科目: 来源: 题型:
查看答案和解析>>【题目】以平面直角坐标系
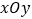 的原点为极点,
的原点为极点,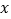 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线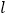 的参数方程为
的参数方程为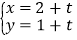 (
(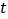 是参数),圆
是参数),圆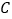 的极坐标方程为
的极坐标方程为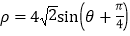 .
.(Ⅰ)求直线
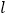 的普通方程与圆
的普通方程与圆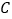 的直角坐标方程;
的直角坐标方程;(Ⅱ)设曲线
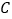 与直线
与直线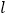 的交于
的交于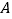 ,
,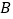 两点,若
两点,若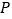 点的直角坐标为
点的直角坐标为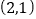 ,求
,求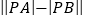 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,角A,B,C对边的边长分别是a,b,c,且a(cosB+cosC)=b+c.
(1)求证:A
 ;
;(2)若△ABC外接圆半径为1,求△ABC周长的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实数m取什么值时,复平面内表示复数z=(m2-8m+15)+(m2-5m-14)i的点.
(1)位于第四象限?
(2)位于第一、三象限?
(3)位于直线y=x上?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是一幅统计图,根据此图得到的以下说法中正确的是( )

A.这几年生活水平逐年得到提高
B.生活费收入指数增长最快的一年是2015年
C.生活价格指数上涨速度最快的一年是2016年
D.虽然2017年的生活费收入增长缓慢,但生活价格指数略有降低,因而生活水平有较大的改善
E.2016年生活价格指数上涨的速度与2017年生活价格指数下降的速度相同
相关试题

