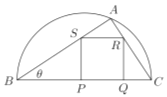
【题目】校园准备绿化一块直径为![]() 的半圆形空地,点
的半圆形空地,点![]() 在半圆圆弧上,△
在半圆圆弧上,△![]() 外的地方种草,△
外的地方种草,△![]() 的内接正方形
的内接正方形![]() 为一水池(
为一水池(![]() ,
,![]() 在
在![]() 边上),其余地方种花,若
边上),其余地方种花,若![]() ,
, ![]() ,设△
,设△![]() 的面积为
的面积为![]() ,正方形面积为
,正方形面积为![]() ;
;
(1)用![]() 和
和![]() 表示
表示![]() 和
和![]() ;
;
(2)当![]() 固定,
固定,![]() 变化时,求
变化时,求![]() 最小值及此时的角
最小值及此时的角![]() ;
;
参考答案:
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() 最小值为
最小值为![]() ,此时
,此时![]() ;
;
【解析】
(1)据题知三角形![]() 为直角三角形,根据三角函数分别求出AC和AB,求出三角形ABC的面积
为直角三角形,根据三角函数分别求出AC和AB,求出三角形ABC的面积![]() ;设正方形
;设正方形![]() 的边长为
的边长为![]() ,利用三角函数分别表示出BS和AS,利用
,利用三角函数分别表示出BS和AS,利用![]() 列出方程求出
列出方程求出![]() ,算出
,算出![]() ;
;
(2)可设![]() 来化简求出
来化简求出![]() 与
与![]() 的比值,利用对勾函数的增减性求出比值的最小值即可求出此时的
的比值,利用对勾函数的增减性求出比值的最小值即可求出此时的![]() .
.
解:(1)在![]() 中,
中,![]() ,
,
![]() ,
,![]() ,
,
设正方形的边长为![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() ,故
,故![]() ,
,
所以![]() ,
,![]() ;
;
(2)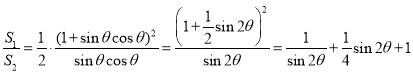 ,
,
令![]() ,因为
,因为![]() ,
,
所以![]() ,则
,则![]() ,
,
所以![]() ,
,
由对勾函数的单调性得:函数![]() 在
在![]() 上递减,
上递减,
因此当![]() 时
时![]() 有最小值
有最小值![]() ,
,
此时![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() 最小,最小值为
最小,最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ).
).(1)若
 在
在 处取到极值,求
处取到极值,求 的值;
的值;(2)若
 在
在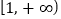 上恒成立,求
上恒成立,求 的取值范围;
的取值范围;(3)求证:当
 时,
时,  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x(lnx-ax)有两个极值点,则实数a的取值范围是( )
A. (-∞,0) B.
 C. (0,1) D. (0,+∞)
C. (0,1) D. (0,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数
 ,定义域为
,定义域为 的函数
的函数 是偶函数,其中
是偶函数,其中 为自然对数的底数.
为自然对数的底数.(Ⅰ)求实数
 值;
值;(Ⅱ)判断该函数
 在
在 上的单调性并用定义证明;
上的单调性并用定义证明;(Ⅲ)是否存在实数
 ,使得对任意的
,使得对任意的 ,不等式
,不等式 恒成立.若存在,求出实数
恒成立.若存在,求出实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, ;
;(1)若
 ,求函数
,求函数 在
在 上的最大值和最小值;
上的最大值和最小值;(2)若函数
 在
在 上既无最大值又无最小值,求角
上既无最大值又无最小值,求角 的范围;
的范围;(3)若函数
 在
在 上有最小值
上有最小值 ,求
,求 的值;
的值; -
科目: 来源: 题型:
查看答案和解析>>【题目】以平面直角坐标系
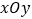 的原点为极点,
的原点为极点,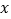 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线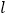 的参数方程为
的参数方程为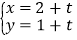 (
(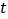 是参数),圆
是参数),圆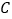 的极坐标方程为
的极坐标方程为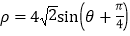 .
.(Ⅰ)求直线
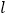 的普通方程与圆
的普通方程与圆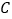 的直角坐标方程;
的直角坐标方程;(Ⅱ)设曲线
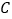 与直线
与直线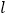 的交于
的交于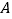 ,
,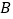 两点,若
两点,若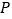 点的直角坐标为
点的直角坐标为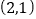 ,求
,求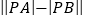 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学调查了某班全部
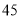 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)参加书法社团
未参加书法社团
参加演讲社团
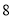
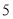
未参加演讲社团

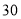
(1)从该班随机选
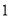 名同学,求该同学至少参加上述一个社团的概率;
名同学,求该同学至少参加上述一个社团的概率;(2)在既参加书法社团又参加演讲社团的
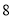 名同学中,有5名男同学
名同学中,有5名男同学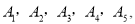
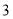 名女同学
名女同学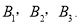 现从这
现从这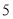 名男同学和
名男同学和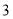 名女同学中各随机选
名女同学中各随机选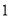 人,求
人,求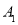 被选中且
被选中且 未被选中的概率.
未被选中的概率.
相关试题

