【题目】已知函数![]()
![]()
(1)当![]() 时,求过点
时,求过点![]() 处的切线方程
处的切线方程
(2)若函数![]() 有两个不同的零点,求
有两个不同的零点,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1) ![]() .
.
(2) ![]() .
.
【解析】分析:(1)求出![]() ,由
,由![]() 的值可得切点坐标,由
的值可得切点坐标,由![]() 的值,可得切线斜率,利用点斜式可得曲线
的值,可得切线斜率,利用点斜式可得曲线![]() 在点
在点![]() 处的切线方程;(2)
处的切线方程;(2)![]()
![]() ,先排除
,先排除![]() 不合题意,当
不合题意,当![]() 时,再讨论两种情况:(i)当
时,再讨论两种情况:(i)当![]() 时,
时, ![]() ,则
,则![]() 无零点,不符合题意,(ii)当
无零点,不符合题意,(ii)当![]() 时,利用函数单调性结合零点存在定理可得
时,利用函数单调性结合零点存在定理可得![]() 在区间
在区间![]() 上有一个零点,
上有一个零点,![]() 在区间
在区间![]() 上有一个零点,从而可得结果.
上有一个零点,从而可得结果.
详解:(1)当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,所以点
,所以点![]()
又由![]() ,得
,得![]() ,
,
所以![]() ,所以切线方程为
,所以切线方程为![]() .
.
(2)函数f(x)的定义域为: ![]() .
.
![]()
![]() ,
,
当a≤0时,易得![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
则![]() 至多只有一个零点,不符合题意,舍去.
至多只有一个零点,不符合题意,舍去.
②当a>0时,令![]() 得: x=a,则
得: x=a,则
|
|
|
|
| + | 0 | - |
| 增 | 极大 | 减 |
∴ 设g(x)=lnx+x-1,∵ 又∵g(1)=0,∴x<1时, g(x)<0; x>1时, g(x)>0. (i)当 不符合题意,舍去 . (ii)当a>1时, ∵ ∵ 设h(x)=lnx-x, (x>1),∵ ∴h(x)在 ∴ ∴f(x)在区间(a,3a-1)上有一个零点,综合知f(x)恰有两个零点. 综上所述,当f(x)有两个不同零点时, a的取值范围是![]() =f(a)=a(lna+a-1)
=f(a)=a(lna+a-1) ![]() ,则g(x)在
,则g(x)在![]() 上单调递增.
上单调递增.![]() 时,
时, ![]() ,则f(x)无零点,
,则f(x)无零点,![]() ,
,![]()
![]() ,∴
,∴![]() 在区间
在区间![]() 上有一个零点,
上有一个零点,![]()
![]()
![]() ,
,![]() ,
,![]() 上单调递减,则
上单调递减,则![]() ,
,![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,直线
 的参数方程为
的参数方程为 (其中
(其中 为参数).现以坐标原点为极点,
为参数).现以坐标原点为极点,  轴的非负半轴为极轴建立极坐标标系,曲线
轴的非负半轴为极轴建立极坐标标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)写出直线
 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;(2)求直线
的直角坐标方程;(2)求直线 被曲线
被曲线 截得的线段的长度.
截得的线段的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组共有12位同学,下图是他们某次数学竞赛成绩(满分100分)的茎叶图,

其中有一个数字模糊不清,图中用
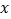 表示,规定成绩不低于80分为优秀.
表示,规定成绩不低于80分为优秀.(1)已知该12位同学竞赛成绩的中位数为78,求图中
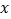 的值;
的值;(2)从该12位同学中随机选3位同学,进行竞赛试卷分析,
设其中成绩优秀的人数为
 ,求
,求 的分布列及数学期望与方差.
的分布列及数学期望与方差. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=a+bx与
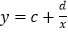 ,若对于任意一点
,若对于任意一点 ,过点
,过点 作与X轴垂直的直线,交函数y=a+bx的图象于点
作与X轴垂直的直线,交函数y=a+bx的图象于点 ,交函数
,交函数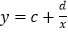 的图象于点
的图象于点 ,定义:
,定义: ,若
,若 则用函数y=a+bx来拟合Y与X之间的关系更合适,否则用函数
则用函数y=a+bx来拟合Y与X之间的关系更合适,否则用函数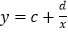 来拟合Y与X之间的关系
来拟合Y与X之间的关系(1)给定一组变量P1(1,4),P2(2,5),p3(3,6),p4(4,5.5),p5(5,5.6),p6(6,5.8),对于函数
 与函数
与函数 ,试利用定义求Q1,Q2的值,并判断哪一个更适合作为点PI(xi,yi)(i=1,2,3…6)中的Y与X之间的拟合函数;
,试利用定义求Q1,Q2的值,并判断哪一个更适合作为点PI(xi,yi)(i=1,2,3…6)中的Y与X之间的拟合函数;(2)若一组变量的散点图符合
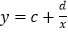 图象,试利用下表中的有关数据与公式求y对x的回归方程, 并预测当
图象,试利用下表中的有关数据与公式求y对x的回归方程, 并预测当 时,
时, 的值为多少.
的值为多少.











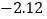
表中的

(附:对于一组数据
 ,其回归直线方程
,其回归直线方程 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为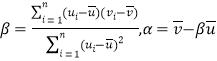 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论中正确的是__________.
①将一组数据中的每个数据都加上或减去同一个常数后,方差不变;
②在吸烟与患肺病这两个分类变量的独立性检验中,“有99%的把握认为吸烟与患肺病有关”的含义是“若某人吸烟,则他有99%的可能患肺病;”
③已知“
 ”为真命题,则“
”为真命题,则“ ”、“
”、“ ”、“
”、“ ”中至少有一个真命题;
”中至少有一个真命题;④以模型
 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设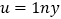 ,其变换后得到线性回归方程
,其变换后得到线性回归方程 则
则 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
 中,
中, 是棱
是棱 的中点.
的中点.
(1)证明:
 平面
平面 ;
;(2)若
 是棱
是棱 的中点,求三棱锥
的中点,求三棱锥 的体积与三棱柱
的体积与三棱柱 的体积之比.
的体积之比. -
科目: 来源: 题型:
查看答案和解析>>【题目】某社区为了解居民喜欢中华传统文化是否与年龄有关,随机调查了60位居民,相关数据统计如下表所示,
喜欢
不喜欢
合计
大于45岁
26
6
32
25岁至45岁
13
15
28
合计
39
21
60
(Ⅰ)是否有99.5%以上的人把握认为喜欢中华传统文化与年龄有关?
(Ⅱ)按年龄采用分层抽样的方法从喜欢中华传统文化的受调查居民中随机抽取6人作进一步了解,若从这6位居民中任选2人,求这2人的年龄均大于45岁的概率.
附:

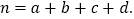

0.025
0.010
0.005
0,001

5.024
6.635
7.879
10.828
相关试题

