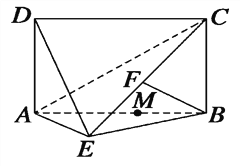
【题目】如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,
BF⊥平面ACE,且点F在CE上.
(1)求证:AE⊥BE;
(2)求三棱锥D—AEC的体积;
(3)设点M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,
使得MN∥平面DAE.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .(3)点N为线段CE上靠近点C的一个三等分点
.(3)点N为线段CE上靠近点C的一个三等分点
【解析】试题分析:(1)先证明![]() ,可得AE⊥平面BCE,由此能证明
,可得AE⊥平面BCE,由此能证明![]() ;(2)由
;(2)由![]() ,能求出三棱锥
,能求出三棱锥![]() 的体积;(3)过点
的体积;(3)过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,推导出
,推导出![]() 平面
平面![]() ,由此能求出当点
,由此能求出当点![]() 为线段
为线段![]() 上靠近点
上靠近点![]() 的一个三等分点时,
的一个三等分点时,![]() 平面
平面![]() .
.
试题解析:(1)证明 由AD⊥平面ABE及AD∥BC,
得BC⊥平面ABE,BC⊥AE,
而BF⊥平面ACE,所以BF⊥AE,
又BC∩BF=B,所以AE⊥平面BCE,
又BE平面BCE,故AE⊥BE.
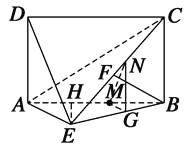
在△ABE中,过点E作EH⊥AB于点H,
则EH⊥平面ACD.
由已知及(1)得EH=![]() AB=
AB=![]() ,S△ADC=2
,S△ADC=2![]() .
.
故VD—AEC=VE—ADC=![]() ×2
×2![]() ×
×![]() =
=![]() .(10分)
.(10分)
(3)解:在△ABE中,过点M作MG∥AE交BE于点G,在△BEC中过点G作GN∥BC交EC于点N,
连结MN,则由![]() =
=![]() =
=![]() =
=![]() ,得CN=
,得CN=![]() CE.
CE.
由MG∥AE,AE平面ADE,
MG平面ADE,则MG∥平面ADE.(12分)
再由GN∥BC,BC∥AD,AD平面ADE,GN平面ADE,
得GN∥平面ADE,所以平面MGN∥平面ADE.
又MN平面MGN,则MN∥平面ADE.(15分)
故当点N为线段CE上靠近点C的一个三等分点时,
MN∥平面ADE.
【方法点晴】本题主要考查线面平行的判定定理、直线和平面成的角的定义及求法、利用等积变换求三棱锥体积,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知三棱锥P-ABC中,∠ACB=90°,CB=4,AB=20,D为AB中点,M为PB中点,且△PDB是正三角形,PA⊥PC。
 .
.(1)求证:DM∥平面PAC;
(2)求证:平面PAC⊥平面ABC;
(3)求三棱锥M-BCD的体积
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某生态园将一三角形地块
 的一角
的一角 开辟为水果园种植桃树,已知角
开辟为水果园种植桃树,已知角 为
为 ,
,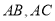 的长度均大于
的长度均大于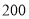 米,现在边界
米,现在边界 处建围墙,在
处建围墙,在 处围竹篱笆.
处围竹篱笆.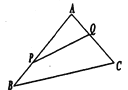
(1)若围墙
 总 长度为
总 长度为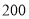 米,如何围可使得三角形地块
米,如何围可使得三角形地块 的面积最大?
的面积最大?(2)已知
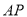 段围墙高
段围墙高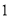 米,
米,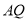 段围墙高
段围墙高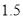 米,造价均为每平方米
米,造价均为每平方米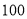 元.若围围墙用了
元.若围围墙用了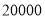 元,问如何围可使竹篱笆用料最省?
元,问如何围可使竹篱笆用料最省? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
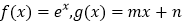 .
.(1)设
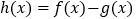 .
.①若函数
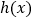 在
在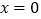 处的切线过点
处的切线过点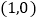 ,求
,求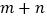 的值;
的值;②当
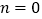 时,若函数
时,若函数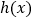 在
在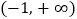 上没有零点,求
上没有零点,求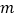 的取值范围.
的取值范围.(2)设函数
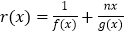 ,且
,且 ,求证: 当
,求证: 当 时,
时,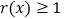 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
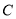 的顶点在原点,焦点在坐标轴上,点
的顶点在原点,焦点在坐标轴上,点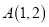 为抛物线
为抛物线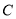 上一点.
上一点.(1)求
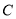 的方程;
的方程;(2)若点
 在
在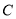 上,过
上,过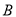 作
作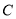 的两弦
的两弦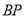 与
与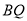 ,若
,若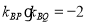 ,求证: 直线
,求证: 直线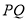 过定点.
过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
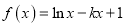 .
.(1)求函数
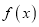 的的单调区间;
的的单调区间;(2)若
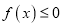 恒成立,试确定实数
恒成立,试确定实数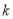 的取值范围;
的取值范围;(3)证明:
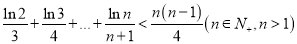 .
. -
科目: 来源: 题型:
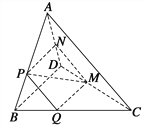
查看答案和解析>>【题目】如图,在四面体ABCD中,截面PQMN是正方形,则下列命题中,正确的为________ (填序号).
①AC⊥BD;②AC∥截面PQMN;③AC=BD;④异面直线PM与BD所成的角为45°.
相关试题

