(12分)已知函数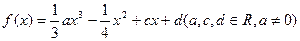 满足
满足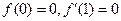 ,且
,且 在
在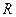 上单调递增.
上单调递增.
(1)求 的解析式;
的解析式;
(2)若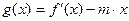 在区间
在区间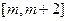 上的最小值为
上的最小值为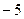 ,求实数
,求实数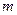 的值.
的值.
参考答案:
解:(1)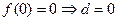 ,故
,故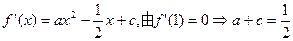
 在
在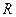 上单调递增
上单调递增
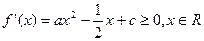
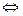
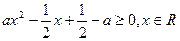
故: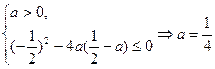 ,于是
,于是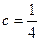
故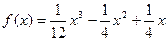 .
.
(2)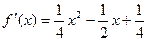 ,故
,故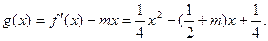
对称轴为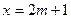 .下面分情况讨论对称轴与区间的位置关系:
.下面分情况讨论对称轴与区间的位置关系:
①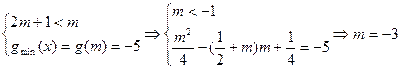 ,(
,(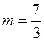 舍去);
舍去);
②当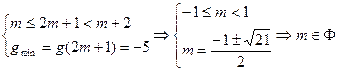 ;
;
③当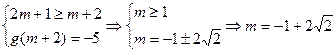 ;
;
综上可得,满足题意的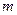 有
有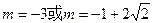 .
.
解析
-
科目: 来源: 题型:解答题
查看答案和解析>>(本题11分)如图,矩形ABCD中,AB=6,BC=2
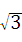 ,点O是AB的中点,点P在AB的延长线
,点O是AB的中点,点P在AB的延长线 上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点
上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点 出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
(1)当等边△EFG的边FG恰好经过点C时,求运动时间t的值;
(2)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积 为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;
为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;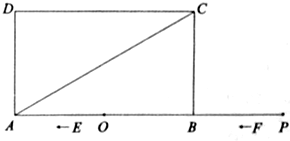
-
科目: 来源: 题型:解答题
查看答案和解析>>某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润与投资单位是万元)
(1)分别将A,B两种产品的利润表示为投资的函数,并写出它们的函数关系式。
(2)该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这10万元投资,才能是企业获得最大利润,其最大利润约为多少万元。( 精确到1万元)。
精确到1万元)。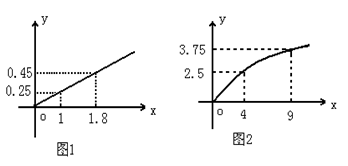
-
科目: 来源: 题型:解答题
查看答案和解析>>
(本小题满分12分)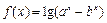 (
(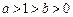 )
)
(1)求 的定义域;
的定义域;
(2)问是否存在实数 、
、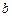 ,当
,当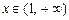 时,
时, 的值域为
的值域为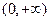 ,且
,且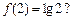 若存在,求出
若存在,求出 、
、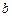 的值,若不存在,说明理由.
的值,若不存在,说明理由. -
科目: 来源: 题型:解答题
查看答案和解析>>(13分)已知函数
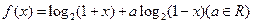 .
.
(1)若f(x )关于原点对称,求a的值;
)关于原点对称,求a的值;
(2)在(1)下,解关于x的不等式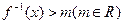 .
. -
科目: 来源: 题型:解答题
查看答案和解析>>(14
 分)某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率
分)某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率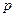 与每日生产产品件数
与每日生产产品件数 (
(
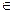
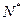 )间的关系为
)间的关系为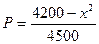 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%)
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%)
(Ⅰ)将日利润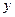 (元)表示成日产量
(元)表示成日产量 (件)的函数;
(件)的函数;
(Ⅱ)求该厂的日产量为多少件时,日利润最大?并求出日利润的最大值 -
科目: 来源: 题型:解答题
查看答案和解析>>(Ⅰ)计算:
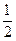 lg2+
lg2+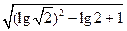 -
-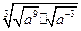 ÷
÷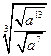 ;
;
(Ⅱ)已知lga+lgb=21g(a-2b),求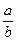 的值.
的值.
相关试题

