【题目】如图,直三棱柱(侧棱与底面垂直的棱柱)ABC﹣A1B1C1中,点G是AC的中点.

(1)求证:B1C∥平面 A1BG;
(2)若AB=BC, ![]() ,求证:AC1⊥A1B.
,求证:AC1⊥A1B.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)连结![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() ,由三角形中位线定理得
,由三角形中位线定理得![]() ,由此能证明
,由此能证明![]() 平面
平面![]() ;(2)由线面垂直得
;(2)由线面垂直得![]() ,由已知推导出
,由已知推导出![]() ,从而得到
,从而得到![]() ,由此能证明
,由此能证明![]() .
.
试题解析:(1)证明:连结AB1,交A1B于点O,连结OG,在△B1AC中,∵G、O分别为AC、AB1中点,∴OG∥B1C,又∵OG平面A1BG,B1C平面A1BG,∴B1C∥平面 A1BG.
(2)证明:∵直三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,BG平面ABC,∴AA1⊥BG,∵G为棱AC的中点,AB=BC,∴BG⊥AC,∵AA1∩AC=A,∴BG⊥平面ACC1A1,∴BG⊥AC1,∵G为棱AC中点,设AC=2,则AG=1,∵![]() ,∴在Rt△ACC1和Rt△A1AG中,
,∴在Rt△ACC1和Rt△A1AG中,![]() ,∴∠AC1C=∠A1GA=∠A1GA+∠C1AC=90°,∴A1G⊥AC1,∵
,∴∠AC1C=∠A1GA=∠A1GA+∠C1AC=90°,∴A1G⊥AC1,∵![]() ,∴AC1⊥平面A1BG,∵A1B平面A1BG,∴AC1⊥A1B.
,∴AC1⊥平面A1BG,∵A1B平面A1BG,∴AC1⊥A1B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
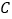 经过点
经过点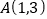 ,
, 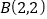 ,并且直线
,并且直线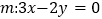 平分圆
平分圆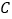 .
.(1)求圆
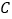 的方程;
的方程;(2)若直线
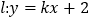 与圆
与圆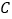 交于
交于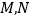 两点,是否存在直线
两点,是否存在直线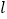 ,使得
,使得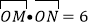 (
(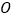 为坐标原点),若存在,求出
为坐标原点),若存在,求出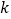 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2sinx(sinx+
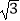 cosx)﹣1(其中x∈R),求:
cosx)﹣1(其中x∈R),求:
(1)函数f(x)的最小正周期;
(2)函数f(x)的单调减区间;
(3)函数f(x)图象的对称轴和对称中心. -
科目: 来源: 题型:
查看答案和解析>>【题目】设直线l的方程为(a+1)x+y+2-a=0(a∈R).
(Ⅰ)若直线l不经过第二象限,求实数a的取值范围;
(Ⅱ)若直线l与两坐标轴围成的三角形面积等于2,求实数a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,已知a=2,b=3,cosC=
 .
.
(1)求△ABC的面积;
(2)求sin(C﹣A)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于100为优品,大于等于90且小于100为合格品,小于90为次品,现随机抽取这两台车床生产的零件各100件进行检测,检测结果统计如下:
测试指标
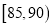
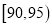
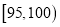
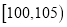
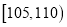
机床甲
8
12
40
32
8
机床乙
7
18
40
29
6
(1)试分别估计甲机床、乙机床生产的零件为优品的概率;
(2)甲机床生产一件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20元;假设甲机床某天生产50件零件,请估计甲机床该天的日利润(单位:元);
(3)从甲、乙机床生产的零件指标在
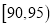 内的零件中,采用分层抽样的方法抽取5件,从这5件中任选2件进行质量分析,求这2件都是乙机床生产的概率.
内的零件中,采用分层抽样的方法抽取5件,从这5件中任选2件进行质量分析,求这2件都是乙机床生产的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校100名学生期中考试数学成绩的频率分布直方图如图:
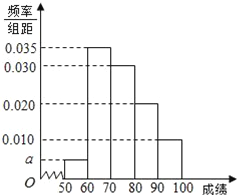
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?
相关试题

