【题目】已知函数 f(x)=ax+lnx,其中a为常数,设e为自然对数的底数.
(1)当a=-1时,求![]() 的最大值;
的最大值;
(2)若f(x)在区间(0,e]上的最大值为-3,求a的值;
(3)当a=-1时,试推断方程![]() 是否有实数解 .
是否有实数解 .
参考答案:
【答案】(1)-1
(2)![]()
(3)方程![]() 无实数解
无实数解
【解析】试题分析:解:(1)当![]() 时,
时,![]()
![]() ,当
,当![]() 时,
时,![]()
![]() 在区间
在区间![]() 上为增函数,
上为增函数,
当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上为减函数,
上为减函数,
所以当![]() ,
,![]() 有最大值,
有最大值,![]() 。 3分
。 3分
(2)∵![]() ,若
,若![]() ,则
,则![]() 在区间(0,e]上恒成立,
在区间(0,e]上恒成立,
![]() 在区间(0,e]上为增函数,
在区间(0,e]上为增函数,![]() ,
,
![]() ,舍去,
,舍去,
当![]() ,
,![]()
![]()
![]() 在区间(0,e]上为增函数,
在区间(0,e]上为增函数,
![]() ,∴
,∴![]() ,舍去,
,舍去,
若![]() ,当
,当![]() 时,
时,![]()
![]() 在区间
在区间![]() 上为增函数,
上为增函数,
当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上为减函数,
上为减函数,
![]() ,
,![]() ;
;
综上![]() 。 8分
。 8分
(3)当![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() ,
,
令![]() ,
,
![]() ,当
,当![]() 时,
时,![]()
![]() 在区间
在区间![]() 上为增函数,
上为增函数,
当![]() 时,
时,![]()
![]() 在区间
在区间![]() 上为减函数,
上为减函数,
当![]() 时,
时,![]() 有最大值
有最大值![]() ,所以
,所以![]() 恒成立,
恒成立,
方程![]() 无实数解。 12分
无实数解。 12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=2
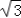 sinxcosx+2cos2x﹣1.
sinxcosx+2cos2x﹣1.(1)求f(x)的最大值,以及该函数取最大值时x的取值集合;
(2)在△ABC中,a、b、c分别是角A、B、C所对的边长,且
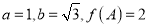 ,求角C.
,求角C. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在棱柱
 的面底是菱形,且
的面底是菱形,且 面ABCD,
面ABCD,  为棱
为棱 的中点,M为线段
的中点,M为线段 的中点.
的中点.(1)求证:平面
 平面
平面 ;
;(2)求三棱锥
 的体积.
的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求不等式
 的解集;
的解集;(2)如果
 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
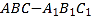 的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是
的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是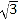 ,
, 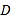 是
是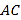 的中点.
的中点.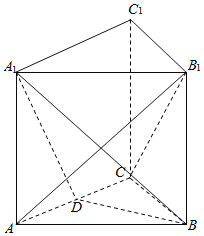
(1)求证:
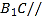 平面
平面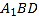 ;
;(2)求二面角
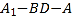 的大小;
的大小;(3)求直线
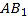 与平面
与平面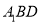 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】过椭圆
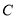 :
: 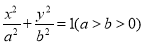 上一点
上一点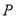 向
向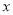 轴作垂线,垂足为右焦点
轴作垂线,垂足为右焦点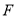 ,
,  、
、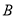 分别为椭圆
分别为椭圆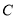 的左顶点和上顶点,且
的左顶点和上顶点,且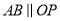 ,
, 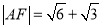 .
.(Ⅰ)求椭圆
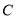 的方程;
的方程;(Ⅱ)若动直线
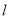 与椭圆
与椭圆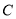 交于
交于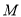 、
、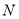 两点,且以
两点,且以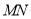 为直径的圆恒过坐标原点
为直径的圆恒过坐标原点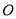 .问是否存在一个定圆与动直线
.问是否存在一个定圆与动直线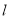 总相切.若存在,求出该定圆的方程;若不存在,请说明理由.
总相切.若存在,求出该定圆的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OQRP为矩形,其中P,Q分别是函数f(x)=
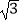 sinwx(A>0,w>0)图象上的一个最高点和最低点,O为坐标原点,R为图象与x轴的交点.
sinwx(A>0,w>0)图象上的一个最高点和最低点,O为坐标原点,R为图象与x轴的交点. 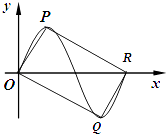
(1)求f(x)的解析式
(2)对于x∈[0,3],方程f2(x)﹣af(x)+1=0恒有四个不同的实数根,求实数a的取值范围
相关试题

