【题目】已知函数y=f1(x),y=f2(x),定义函数f(x) .
.
(1)设函数f1(x)=x+3,f2(x)=x2﹣x,求函数y=f(x)的解析式;
(2)在(1)的条件下,g(x)=mx+2(m∈R),函数h(x)=f(x)﹣g(x)有三个不同的零点,求实数m的取值范围;
(3)设函数f1(x)=x2﹣2,f2(x)=|x﹣a|,函数F(x)=f1(x)+f2(x),求函数F(x)的最小值.
参考答案:
【答案】(1)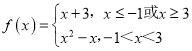 ;(2)
;(2)![]() ;(3)
;(3)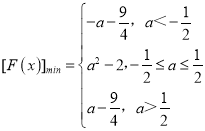
【解析】
(1)根据函数f(x)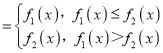 的定义,两个函数中取小的.
的定义,两个函数中取小的.
(2)函数h(x)=f(x)﹣g(x)有三个不同的零点,即方程f(x)=g(x)有三个不同的实数根,因为函数![]() 是分段函数,分类讨论,分别用一次方程和二次方程求解.
是分段函数,分类讨论,分别用一次方程和二次方程求解.
(3)根据题意F(x)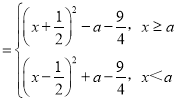 .按照二次函数函数定区间动的类型,讨论对称轴与区间端点值间的关系求最值.
.按照二次函数函数定区间动的类型,讨论对称轴与区间端点值间的关系求最值.
(1)∵f1(x)=x+3,![]() ,
,
当f1(x)≤f2(x),即x≥3或x≤﹣1时,f(x)=x+3,
当f1(x)>f2(x),即﹣1<x<3时,![]() ,
,
综上: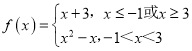 .
.
(2)函数h(x)=f(x)﹣g(x)有三个不同的零点,
即方程f(x)=g(x)有三个不同的实数根,
因为函数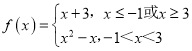 ,函数g(x)=mx+2(m∈R),
,函数g(x)=mx+2(m∈R),
所以当x≤﹣1或x≥3时,mx+2=x+3恰有一个实数解,
所以![]() 或
或![]() ,
,
解得,![]() .
.
当﹣1<x<3时,mx+2=x2﹣x恰有两个不同的实数解,
即当﹣1<x<3时x2﹣(m+1)x﹣2=0恰有两个不同的实数解,
设函数h(x)=x2﹣(m+1)x﹣2,
由题意可得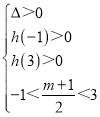 ,
,
所以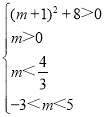 ,
,
解得![]() ,
,
综上,m的取值范围为![]() .
.
(3)F(x)=f1(x)+f2(x)=x2+|x﹣a|﹣2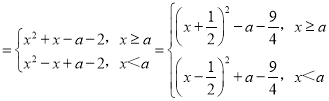 .
.
①若a![]() ,则函数F(x)在
,则函数F(x)在![]() 上是单调减函数,在
上是单调减函数,在![]() 上是单调增函数,
上是单调增函数,
此时,函数F(x)的最小值为![]() ;
;
②若![]() ,则函数F(x)在(﹣∞,a)上是单调减函数,在(a,+∞)上是单调增函数,
,则函数F(x)在(﹣∞,a)上是单调减函数,在(a,+∞)上是单调增函数,
此时,函数F(x)的最小值为F(a)=a2﹣2;
③若![]() ,则函数F(x)在
,则函数F(x)在![]() 上是单调减函数,在
上是单调减函数,在![]() 上是单调增函数,
上是单调增函数,
此时,函数F(x)的最小值为![]() ;
;
综上: .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在底面边长为
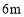 、高为
、高为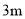 的正六棱柱
的正六棱柱 展厅内,长为
展厅内,长为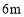 ,宽为
,宽为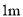 的矩形油画
的矩形油画 挂在厅内正前方中间.
挂在厅内正前方中间.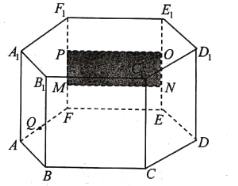
(1)求证:平面
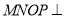 平面
平面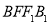 ;
;(2)当游客
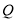 在
在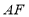 上看油画的纵向视角(即
上看油画的纵向视角(即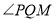 )最大时,求
)最大时,求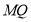 与油画平面所成的角.
与油画平面所成的角. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
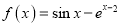 ,求证:
,求证:(1)
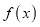 在区间
在区间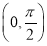 存在唯一极大值点;
存在唯一极大值点;(2)
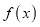 在
在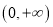 上有且仅有2个零点.
上有且仅有2个零点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知奇函数f(x)
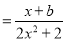 ,函数g(θ)=cos2θ+2sinθ
,函数g(θ)=cos2θ+2sinθ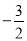 ,θ∈[m,
,θ∈[m,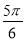 ].m,b∈R.
].m,b∈R.(1)求b的值;
(2)判断函数f(x)在[0,1]上的单调性,并证明;
(3)当x∈[0,1]时,函数g(θ)的最小值恰为f(x)的最大值,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大西洋鲑鱼每年都要逆流而上,游回产地产卵,研究鲑鱼的科学家发现鲑鱼的游速
 (单位:
(单位:  )与其耗氧量单位数
)与其耗氧量单位数 之间的关系可以表示为函数
之间的关系可以表示为函数 ,其中
,其中 为常数,已知一条鲑鱼在静止时的耗氧量为100个单位;而当它的游速为
为常数,已知一条鲑鱼在静止时的耗氧量为100个单位;而当它的游速为 时,其耗氧量为2700个单位.
时,其耗氧量为2700个单位.(1)求出游速
 与其耗氧量单位数
与其耗氧量单位数 之间的函数解析式;
之间的函数解析式;(2)求当一条鲑鱼的游速不高于
 时,其耗氧量至多需要多少个单位?
时,其耗氧量至多需要多少个单位? -
科目: 来源: 题型:
查看答案和解析>>【题目】某高中在校学生2000人
 为了响应“阳光体育运动”号召,学校举行了跑步和登山比赛活动
为了响应“阳光体育运动”号召,学校举行了跑步和登山比赛活动 每人都参加而且只参与了其中一项比赛,各年级参与比赛人数情况如表:
每人都参加而且只参与了其中一项比赛,各年级参与比赛人数情况如表:高一年级
高二年级
高三年级
跑步
a
b
c
登山
x
y
z
其中a:b:
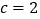 :3:5,全校参与登山的人数占总人数的
:3:5,全校参与登山的人数占总人数的 ,为了了解学生对本次活动的满意程度,现用分层抽样方式从中抽取一个100个人的样本进行调查,则高二年级参与跑步的学生中应抽取
,为了了解学生对本次活动的满意程度,现用分层抽样方式从中抽取一个100个人的样本进行调查,则高二年级参与跑步的学生中应抽取

A. 6人B. 12人C. 18人D. 24人
-
科目: 来源: 题型:
查看答案和解析>>【题目】给定两个七棱锥,它们有公共面的底面
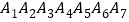 ,顶点
,顶点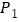 、
、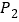 在底面的两则.现将下述线段中的每一条染红、蓝两色之一:
在底面的两则.现将下述线段中的每一条染红、蓝两色之一: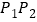 ,底面上的所有对角线和所有的侧棱.求证:图中心存在一个同色三角形.
,底面上的所有对角线和所有的侧棱.求证:图中心存在一个同色三角形.
相关试题

