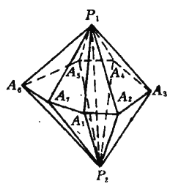
【题目】给定两个七棱锥,它们有公共面的底面![]() ,顶点
,顶点![]() 、
、![]() 在底面的两则.现将下述线段中的每一条染红、蓝两色之一:
在底面的两则.现将下述线段中的每一条染红、蓝两色之一:![]() ,底面上的所有对角线和所有的侧棱.求证:图中心存在一个同色三角形.
,底面上的所有对角线和所有的侧棱.求证:图中心存在一个同色三角形.
参考答案:
【答案】见解析
【解析】
先证明一个引理:
引理 若同侧的7条侧棱![]() 中有5条同色,则命题成立.
中有5条同色,则命题成立.
证明:在所述条件下,必有两两不相邻的三条侧棱![]() ,
,![]() ,
,![]() 同侧,不妨设同为红色,则在三条对角线
同侧,不妨设同为红色,则在三条对角线![]() ,
,![]() ,
,![]() 中,若有一条是红色,则有一个红色三角形;若三条都为蓝色,则
中,若有一条是红色,则有一个红色三角形;若三条都为蓝色,则![]() 本身即为单色三角形,引理得证.
本身即为单色三角形,引理得证.
现在回到原题.
不妨设![]() .染红色.考虑所有的有序对
.染红色.考虑所有的有序对![]() (
(![]() 的颜色,
的颜色,![]() 的颜色)(
的颜色)(![]() ),其必为(红,红),(红,蓝),(蓝,红),(蓝,蓝)之一.
),其必为(红,红),(红,蓝),(蓝,红),(蓝,蓝)之一.
若某个![]() 为(红,红),则
为(红,红),则![]() 为单色三角形.
为单色三角形.
若无某个![]() 为(红,红),则由抽屉原则,存在
为(红,红),则由抽屉原则,存在![]() ,使得
,使得![]() .分两种情况:
.分两种情况:
(1)若它们为(红,蓝)或(蓝,红),则易出![]() ,
,![]() ,
,![]() 中必有两点不相邻(设为
中必有两点不相邻(设为![]() 和
和![]() )知,
)知,![]() 无论染何种颜色,图中都有一个单色三角形.
无论染何种颜色,图中都有一个单色三角形.
(2)为了避免发生(1)的情况,只能![]() (红,蓝)
(红,蓝)![]() (蓝,红)
(蓝,红)![]() ,于是由
,于是由![]() ,
,![]() 引出异于
引出异于![]() 的蓝边都为5条,由引理知命题成立.
的蓝边都为5条,由引理知命题成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=f1(x),y=f2(x),定义函数f(x)
 .
.(1)设函数f1(x)=x+3,f2(x)=x2﹣x,求函数y=f(x)的解析式;
(2)在(1)的条件下,g(x)=mx+2(m∈R),函数h(x)=f(x)﹣g(x)有三个不同的零点,求实数m的取值范围;
(3)设函数f1(x)=x2﹣2,f2(x)=|x﹣a|,函数F(x)=f1(x)+f2(x),求函数F(x)的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大西洋鲑鱼每年都要逆流而上,游回产地产卵,研究鲑鱼的科学家发现鲑鱼的游速
 (单位:
(单位:  )与其耗氧量单位数
)与其耗氧量单位数 之间的关系可以表示为函数
之间的关系可以表示为函数 ,其中
,其中 为常数,已知一条鲑鱼在静止时的耗氧量为100个单位;而当它的游速为
为常数,已知一条鲑鱼在静止时的耗氧量为100个单位;而当它的游速为 时,其耗氧量为2700个单位.
时,其耗氧量为2700个单位.(1)求出游速
 与其耗氧量单位数
与其耗氧量单位数 之间的函数解析式;
之间的函数解析式;(2)求当一条鲑鱼的游速不高于
 时,其耗氧量至多需要多少个单位?
时,其耗氧量至多需要多少个单位? -
科目: 来源: 题型:
查看答案和解析>>【题目】某高中在校学生2000人
 为了响应“阳光体育运动”号召,学校举行了跑步和登山比赛活动
为了响应“阳光体育运动”号召,学校举行了跑步和登山比赛活动 每人都参加而且只参与了其中一项比赛,各年级参与比赛人数情况如表:
每人都参加而且只参与了其中一项比赛,各年级参与比赛人数情况如表:高一年级
高二年级
高三年级
跑步
a
b
c
登山
x
y
z
其中a:b:
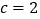 :3:5,全校参与登山的人数占总人数的
:3:5,全校参与登山的人数占总人数的 ,为了了解学生对本次活动的满意程度,现用分层抽样方式从中抽取一个100个人的样本进行调查,则高二年级参与跑步的学生中应抽取
,为了了解学生对本次活动的满意程度,现用分层抽样方式从中抽取一个100个人的样本进行调查,则高二年级参与跑步的学生中应抽取

A. 6人B. 12人C. 18人D. 24人
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
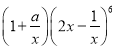 的展开式中各项系数的和为2,则下列结论正确的有( )
的展开式中各项系数的和为2,则下列结论正确的有( )A.
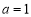
B.展开式中常数项为160
C.展开式系数的绝对值的和1458
D.若
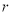 为偶数,则展开式中
为偶数,则展开式中 和
和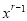 的系数相等
的系数相等 -
科目: 来源: 题型:
查看答案和解析>>【题目】2018年中秋季到来之际,某超市为了解中秋节期间月饼的销售量,对其所在销售范围内的1000名消费者在中秋节期间的月饼购买量(单位:
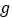 )进行了问卷调查,得到如下频率分布直方图:
)进行了问卷调查,得到如下频率分布直方图:
(1)求频率分布直方图中
 的值;
的值;(2)已知该超市所在销售范围内有20万人,并且该超市每年的销售份额约占该市场总量的
 ,请根据人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求?
,请根据人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求?(3)由频率分布直方图可以认为,该销售范围内消费者的月饼购买量
 服从正态分布
服从正态分布 ,其中样本平均数
,其中样本平均数 作为
作为 的估计值,样本标准差
的估计值,样本标准差 作为
作为 的估计值,设
的估计值,设 表示从该销售范围内的消费者中随机抽取10名,其月饼购买量位于
表示从该销售范围内的消费者中随机抽取10名,其月饼购买量位于 的人数,求
的人数,求 的数学期望.
的数学期望.附:经计算得
 ,若随机变量
,若随机变量 服从正态分布
服从正态分布 ,则
,则 ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
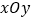 中,椭圆
中,椭圆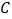 的中心在原点,焦点在
的中心在原点,焦点在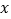 轴上,且过点
轴上,且过点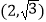 ,若
,若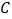 的两焦点与其中一个顶点能构成一个等边三角形.
的两焦点与其中一个顶点能构成一个等边三角形.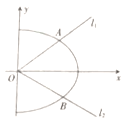
(1)求
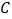 的方程.
的方程.(2)已知过
 的两条直线
的两条直线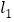 ,
,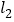 (斜率都存在)与
(斜率都存在)与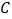 的右半部分(
的右半部分(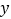 轴右侧)分别相交于
轴右侧)分别相交于 ,
,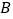 两点,且
两点,且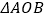 的面积为
的面积为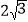 ,试判断
,试判断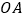 ,
,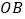 的斜率之积是否为定值?若是,求出定值;若不是,说明理由.
的斜率之积是否为定值?若是,求出定值;若不是,说明理由.
相关试题

