【题目】甲、乙两支篮球队赛季总决赛采用7场4胜制,每场必须分出胜负,场与场之间互不影响,只要有一队获胜4场就结束比赛.现已比赛了4场,且甲篮球队胜3场.已知甲球队第5,6场获胜的概率均为![]() ,但由于体力原因,第7场获胜的概率为
,但由于体力原因,第7场获胜的概率为![]() .
.
(1)求甲队分别以![]() ,
,![]() 获胜的概率;
获胜的概率;
(2)设![]() 表示决出冠军时比赛的场数,求
表示决出冠军时比赛的场数,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考答案:
【答案】(1)![]() ,
,![]() ;
;
(2)X的分布列为
X | 5 | 6 | 7 |
|
|
|
|
![]() .
.
【解析】
(1)记甲队以![]() ,
,![]() 获胜的事件分别为A,B,事件
获胜的事件分别为A,B,事件![]() 说明第五场甲负,第六场甲胜,因此
说明第五场甲负,第六场甲胜,因此![]() ,事件
,事件![]() 说明第五、六两场甲都负,第七场 甲胜,因此
说明第五、六两场甲都负,第七场 甲胜,因此![]() ;(2)从题设可知
;(2)从题设可知![]() 的取舍分别5,6,7,可分别求出相应的概率,得分布列.
的取舍分别5,6,7,可分别求出相应的概率,得分布列.
(1)设甲队以![]() ,
,![]() 获胜的事件分别为A,B,
获胜的事件分别为A,B,
∵甲队第5,6场获胜的概率均为![]() ,第7场获胜的概率为
,第7场获胜的概率为![]() ,
,
∴![]() ,
,![]() ,
,
∴甲队以![]() ,
,![]() 获胜的概率分别为
获胜的概率分别为![]() 和
和![]() .
.
(2)随机变量X的可能取值为5,6,7,
∴![]() ,
,![]()
![]() ,
,![]()
![]() ,
,
∴随机变量X的分布列为
X | 5 | 6 | 7 |
|
|
|
|
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]
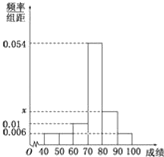
(Ⅰ)求图中
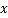 的值,并估计该班期中考试数学成绩的众数;
的值,并估计该班期中考试数学成绩的众数;(Ⅱ)从成绩不低于90分的学生和成绩低于50分的学生中随机选取2人,求这2人成绩均不低于90分的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地某路无人驾驶公交车发车时间间隔
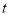 (单位:分钟)满足
(单位:分钟)满足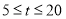 ,
,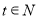 .经测算,该路无人驾驶公交车载客量
.经测算,该路无人驾驶公交车载客量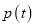 与发车时间间隔
与发车时间间隔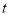 满足:
满足: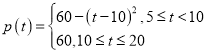 ,其中
,其中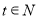 .
.(1)求
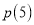 ,并说明
,并说明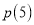 的实际意义;
的实际意义;(2)若该路公交车每分钟的净收益
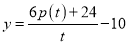 (元),问当发车时间间隔为多少时,该路公交车每分钟的净收益最大?并求每分钟的最大净收益.
(元),问当发车时间间隔为多少时,该路公交车每分钟的净收益最大?并求每分钟的最大净收益. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解高一新生对文理科的选择,对1 000名高一新生发放文理科选择调查表,统计知,有600名学生选择理科,400名学生选择文科.分别从选择理科和文科的学生随机各抽取20名学生的数学成绩得如下累计表:
分数段
理科人数
文科人数






正
正
正


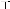
(1)从统计表分析,比较选择文理科学生的数学平均分及学生选择文理科的情况,并绘制理科数学成绩的频率分布直方图.

(2)根据你绘制的频率分布直方图,估计意向选择理科的学生的数学成绩的中位数与平均分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知参加某项活动的六名成员排成一排合影留念,且甲乙两人均在丙领导人的同侧,则不同的排法共有( )
A. 240种 B. 360种 C. 480种 D. 600种
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为椭圆
为椭圆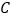 的左、右顶点,
的左、右顶点,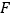 为其右焦点,
为其右焦点,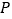 是椭圆
是椭圆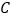 上异于
上异于 的动点,且
的动点,且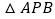 面积的最大值为
面积的最大值为 .
.(1)求椭圆
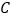 的方程;
的方程;(2)直线
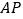 与椭圆在点
与椭圆在点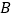 处的切线交于点
处的切线交于点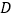 ,当点
,当点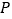 在椭圆上运动时,求证:以
在椭圆上运动时,求证:以  为直径的圆与直线
为直径的圆与直线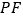 恒相切.
恒相切. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,长度为3的线段
 的端点
的端点 、
、 分别在
分别在 ,
, 轴上滑动,点
轴上滑动,点 在线段
在线段 上,且
上,且 ,
,(1)若点
 的轨迹为曲线
的轨迹为曲线 ,求其方程;
,求其方程;(2)过点
 的直线
的直线 与曲线
与曲线 交于不同两点
交于不同两点 、
、 ,
, 是曲线上不同于
是曲线上不同于 、
、 的动点,求
的动点,求 面积的最大值.
面积的最大值.
相关试题

