【题目】如图,在△ABC中,已知|AB|=4 ![]() ,且三内角A,B,C满足2sin A+sin C=2sin B,建立适当的坐标系,求顶点C的轨迹方程.
,且三内角A,B,C满足2sin A+sin C=2sin B,建立适当的坐标系,求顶点C的轨迹方程.
参考答案:
【答案】![]()
【解析】试题分析:先根据条件建立直角坐标系,根据正弦定理将角的关系转化为边的关系,再利用双曲线定义确定轨迹,并根据基本量求轨迹方程
试题解析:解:以AB边所在直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系(如图所示).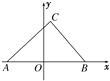 则A(-2
则A(-2![]() ,0),B(2
,0),B(2![]() ,0).设边BC、AC、AB的长分别为a、b、c,由正弦定理得sin A=
,0).设边BC、AC、AB的长分别为a、b、c,由正弦定理得sin A=![]() ,sin B=
,sin B=![]() ,sin C=
,sin C=![]() (R为△ABC外接圆的半径).
(R为△ABC外接圆的半径).
∵2sin A+sin C=2sin B,∴2a+c=2b,即b-a=![]() .
.
从而有|CA|-|CB|=![]() |AB|=2
|AB|=2 ![]() <|AB|.
<|AB|.
由双曲线的定义知,点C的轨迹为双曲线的右支(除去与x轴的交点).∵a=![]() ,c=2
,c=2![]() ,∴b2=6.
,∴b2=6.
∴顶点C的轨迹方程为![]() -
-![]() =1(x>
=1(x>![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在极坐标系下,已知圆O:ρ=cosθ+sinθ和直线l:ρsin(θ﹣
 )=
)= 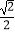 .
.
(1)求圆O和直线l的直角坐标方程;
(2)当θ∈(0,π)时,求直线l与圆O公共点的极坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=|ax+1|(a∈R),不等式f(x)≤3的解集为{x|﹣2≤x≤1}. (Ⅰ)求a的值;
(Ⅱ)若f(x)﹣2f( )≤k恒成立,求k的取值范围.
)≤k恒成立,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形
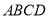 中,
中, 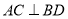 ,
, 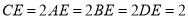 ,将四边形
,将四边形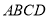 沿着
沿着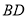 折叠,得到图2所示的三棱锥
折叠,得到图2所示的三棱锥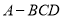 ,其中
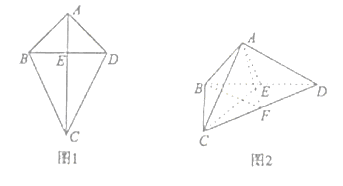
,其中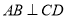 .
.
(1)证明:平面
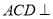 平面
平面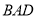 ;
;(2)若
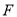 为
为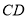 中点,求二面角
中点,求二面角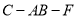 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若要按从大到小给7,5,9,3,10五个数排序,试写出算法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出如图所示的对应:
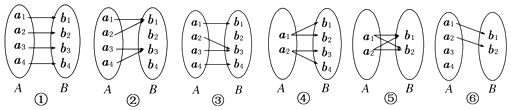
其中构成从A到B的映射的个数为( )
A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>0,a≠1.设命题p:函数y=loga(x+1)在(0,+∞)内单调递减;命题q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.若p或q为真,p且q为假,求a的取值范围.
相关试题

