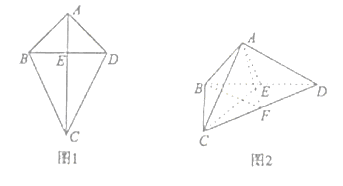
【题目】如图1,四边形![]() 中,
中, ![]() ,
, ![]() ,将四边形
,将四边形![]() 沿着
沿着![]() 折叠,得到图2所示的三棱锥
折叠,得到图2所示的三棱锥![]() ,其中
,其中![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 中点,求二面角
中点,求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析: (1)由面面垂直的判定定理得出证明; (2)以E为原点,建立空间直角坐标系,写出各点坐标,设![]() ,由
,由![]() ,求出
,求出![]() ,求出平面
,求出平面![]() 的一个法向量,由已知条件找出平面
的一个法向量,由已知条件找出平面![]() 的一个法向量,利用公式求出二面角
的一个法向量,利用公式求出二面角![]() 的余弦值.
的余弦值.
试题解析:(Ⅰ)因为![]() 且
且![]() ,可得
,可得![]() 为等腰直角三角形,
为等腰直角三角形,
则![]() ,又
,又![]() ,且
,且![]() 平面
平面![]() ,
, ![]() ,
,
故![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(Ⅱ)以![]() 为原点,以
为原点,以![]() 的方向为
的方向为![]() 轴正方向,
轴正方向, ![]() 的方向为
的方向为![]() 轴正方向,建立如图所示的空间直角坐标系.
轴正方向,建立如图所示的空间直角坐标系.
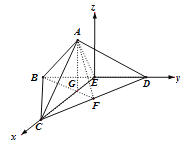
过![]() 点作平面
点作平面![]() 的垂线,垂足为
的垂线,垂足为![]() ,根据对称性,显然
,根据对称性,显然![]() 点在
点在![]() 轴上,设
轴上,设![]() .由题设条件可得下列坐标:
.由题设条件可得下列坐标: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.![]() ,
, ![]() ,由于
,由于![]() ,所以
,所以![]() ,解得
,解得![]() ,则
,则![]() 点坐标为
点坐标为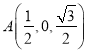 . 由于
. 由于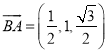 ,
, ![]() ,设平面
,设平面![]() 的法向量
的法向量![]() ,
,
由![]() 及
及![]() 得
得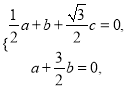
令![]() ,由此可得
,由此可得![]() .
.
由于![]() ,
, ![]() ,则
,则![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则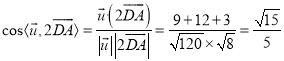 ,
,
因为二面角![]() 为锐角,
为锐角,
则二面角![]() 的余弦值为
的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
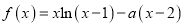 .
.(1)若
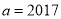 ,求曲线
,求曲线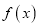 在
在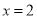 处的切线方程;
处的切线方程;(2)若当
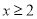 时,
时, 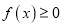 ,求
,求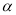 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在极坐标系下,已知圆O:ρ=cosθ+sinθ和直线l:ρsin(θ﹣
 )=
)= 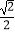 .
.
(1)求圆O和直线l的直角坐标方程;
(2)当θ∈(0,π)时,求直线l与圆O公共点的极坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=|ax+1|(a∈R),不等式f(x)≤3的解集为{x|﹣2≤x≤1}. (Ⅰ)求a的值;
(Ⅱ)若f(x)﹣2f( )≤k恒成立,求k的取值范围.
)≤k恒成立,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知|AB|=4
 ,且三内角A,B,C满足2sin A+sin C=2sin B,建立适当的坐标系,求顶点C的轨迹方程.
,且三内角A,B,C满足2sin A+sin C=2sin B,建立适当的坐标系,求顶点C的轨迹方程.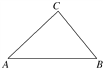
-
科目: 来源: 题型:
查看答案和解析>>【题目】若要按从大到小给7,5,9,3,10五个数排序,试写出算法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出如图所示的对应:
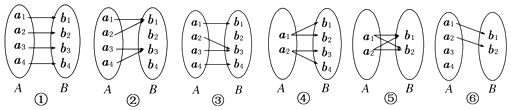
其中构成从A到B的映射的个数为( )
A.3
B.4
C.5
D.6
相关试题

