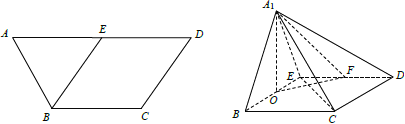
【题目】如图1,在等腰梯形![]() 中,
中,![]() ,
,![]() 为
为![]() 中点, 点
中点, 点![]() 分别为
分别为![]() 的中点, 将
的中点, 将![]() 沿
沿![]() 折起到
折起到 ![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() (如图
(如图 ![]() ).
).


(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)侧棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)要证![]() ,只需证明
,只需证明![]() 平面
平面![]() 即可;(2)以
即可;(2)以![]() 为原点,
为原点,![]() 分别为
分别为![]() 轴建立空间直角坐标系,设平面
轴建立空间直角坐标系,设平面![]() 的一个法向量为
的一个法向量为![]() ,根据法向量与平面的两个向量的数量积为零,解得
,根据法向量与平面的两个向量的数量积为零,解得![]() ,进而可求解直线
,进而可求解直线![]() 与平面
与平面![]() 所成角的正弦值;(3)假设在侧棱
所成角的正弦值;(3)假设在侧棱![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,设
,设![]() ,由四边形
,由四边形![]() 为菱形,且
为菱形,且![]() ,结合(1)可知,
,结合(1)可知,![]() 平面
平面![]() ,得到
,得到![]() 为平面
为平面![]() 的一个法向量.据此可求解
的一个法向量.据此可求解![]() 的值.
的值.
试题解析:(1)如图1,在等腰梯形![]() 中, 由
中, 由![]() 为
为![]() 中点, 所以
中点, 所以![]() 为等边三角形.如图2, 因为
为等边三角形.如图2, 因为![]() 为
为![]() 的中点,
的中点,
所以![]() 又因为平面
又因为平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)连结![]() ,由已知得
,由已知得![]() ,又
,又![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
由(1)知![]() 平面
平面![]() ,所以
,所以![]() 两两垂直,
两两垂直,
以![]() 为原点,
为原点,![]() 分别为
分别为![]() 轴建立空间直角坐标系(如图).
轴建立空间直角坐标系(如图).
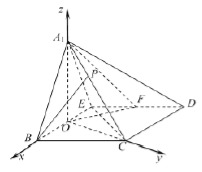
因为![]() ,易知
,易知![]() ,
,
![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由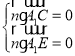 ,得
,得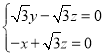 ,即
,即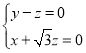 ,取
,取![]() ,得
,得![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则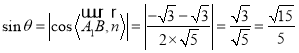 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(3)假设在侧棱![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,设
,设![]() ,
,
因为![]() ,
,
所以![]() .
.
易证四边形![]() 为菱形,且
为菱形,且![]() ,
,
又由(1)可知,![]() 平面
平面![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
由![]() ,得
,得![]() ,
,
所以侧棱![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在边长为1的等边三角形
 中,
中, 分别是
分别是 边上的点,
边上的点, ,
, 是
是 的中点,
的中点, 与
与 交于点
交于点 ,将
,将 沿
沿 折起,得到如图2所示的三棱锥
折起,得到如图2所示的三棱锥 ,其中
,其中 .
.(1) 证明:
 //平面
//平面 ;
; (2) 证明:

 平面
平面 ;
;(3) 当
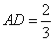 时,求三棱锥
时,求三棱锥 的体积
的体积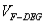 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在甲、乙等7个选手参加的一次演讲比赛中,采用抽签的方式随机确定每个选手的演出顺序(序号为1,2,……7),求:
(1)甲、乙两个选手的演出序号至少有一个为奇数的概率;
(2)甲、乙两选手之间的演讲选手个数
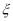 的分布列与期望.
的分布列与期望. -
科目: 来源: 题型:
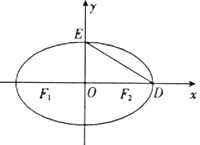
查看答案和解析>>【题目】如图,
 为椭圆
为椭圆 的左右焦点,
的左右焦点,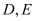 是椭圆的两个顶点,
是椭圆的两个顶点,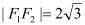 ,
, ,若点
,若点 在椭圆
在椭圆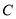 上,则点
上,则点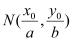 称为点
称为点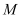 的一个“椭点”.直线
的一个“椭点”.直线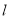 与椭圆交于
与椭圆交于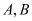 两点,
两点,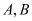 两点的“椭点”分别为
两点的“椭点”分别为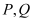 ,已知以
,已知以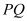 为直径的圆经过坐标原点
为直径的圆经过坐标原点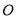 .
.
(1)求椭圆
 的标准方程;
的标准方程;(2)试探讨
 的面积
的面积 是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
是否为定值?若为定值,求出该定值;若不为定值,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
 中,底面
中,底面 为菱形,侧面
为菱形,侧面 为等边三角形,且侧面
为等边三角形,且侧面 底面
底面 ,
,  ,
,  分别为
分别为 ,
,  的中点.
的中点.(Ⅰ)求证:
 .
.(Ⅱ)求证:平面
 平面
平面 .
.(Ⅲ)侧棱
 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】文科做:数列
 中,
中, 且满足
且满足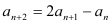
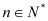
(I)求数列
 的通项公式;
的通项公式;(II)设
 ,求
,求 ;
;(III)设
 =
=
 ,是否存在最大的整数
,是否存在最大的整数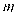 ,使得对任意
,使得对任意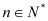 ,均有
,均有
 成立?若存在,求出
成立?若存在,求出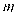 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在等比数列{an}中,a1=2,a3,a2+a4,a5成等差数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1+
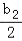 +…+
+…+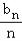 =an(n∈N*),{bn}的前n项和为Sn,求使Sn﹣nan+6≥0成立的正整数n的最大值.
=an(n∈N*),{bn}的前n项和为Sn,求使Sn﹣nan+6≥0成立的正整数n的最大值.
相关试题

