【题目】在甲、乙等7个选手参加的一次演讲比赛中,采用抽签的方式随机确定每个选手的演出顺序(序号为1,2,……7),求:
(1)甲、乙两个选手的演出序号至少有一个为奇数的概率;
(2)甲、乙两选手之间的演讲选手个数![]() 的分布列与期望.
的分布列与期望.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)由题意设A表示“甲、乙的演出序号至少有一个为奇数”,则.![]() 表示“甲、乙的演出序号均为偶数”,则由等可能性事件的概率计算公式即可求得;(2)由于题意知道ξ表示甲、乙两选手之间的演讲选手个数,有题意则ξ的可能取值为0,1,2,3,4,5,再有古典概型随机事件的概率公式及离散型随机变量的定义与其分布列即可求得
表示“甲、乙的演出序号均为偶数”,则由等可能性事件的概率计算公式即可求得;(2)由于题意知道ξ表示甲、乙两选手之间的演讲选手个数,有题意则ξ的可能取值为0,1,2,3,4,5,再有古典概型随机事件的概率公式及离散型随机变量的定义与其分布列即可求得
试题解析:(1)设![]() 表示“甲、乙的演出序号至少有一个为奇数”,则
表示“甲、乙的演出序号至少有一个为奇数”,则![]() 表示 “甲、乙的演出序号均为偶数”.由等可能性事件的概率计算公式得
表示 “甲、乙的演出序号均为偶数”.由等可能性事件的概率计算公式得
![]() .
.
(2)![]() 的可能取值为
的可能取值为![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() …………11分
…………11分
从而![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
|
所以,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中秋节到了,糕点店的售货员很忙,请设计一个程序,帮助售货员算账,已知豆沙馅的月饼每千克25元,蛋黄馅的月饼每千克35元,莲蓉馅的月饼每千克30元,那么依次购买这三种月饼a、b、c千克,应收多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若两个平面与第三个平面相交,有两条交线且两条交线互相平行,则这两个平面( )
A.有公共点
B.没有公共点
C.平行
D.平行或相交 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在边长为1的等边三角形
 中,
中, 分别是
分别是 边上的点,
边上的点, ,
, 是
是 的中点,
的中点, 与
与 交于点
交于点 ,将
,将 沿
沿 折起,得到如图2所示的三棱锥
折起,得到如图2所示的三棱锥 ,其中
,其中 .
.(1) 证明:
 //平面
//平面 ;
; (2) 证明:

 平面
平面 ;
;(3) 当
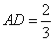 时,求三棱锥
时,求三棱锥 的体积
的体积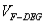 .
.
-
科目: 来源: 题型:
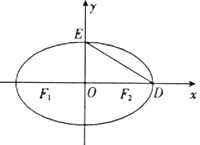
查看答案和解析>>【题目】如图,
 为椭圆
为椭圆 的左右焦点,
的左右焦点,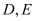 是椭圆的两个顶点,
是椭圆的两个顶点,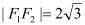 ,
, ,若点
,若点 在椭圆
在椭圆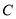 上,则点
上,则点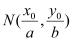 称为点
称为点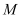 的一个“椭点”.直线
的一个“椭点”.直线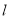 与椭圆交于
与椭圆交于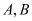 两点,
两点,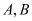 两点的“椭点”分别为
两点的“椭点”分别为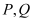 ,已知以
,已知以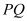 为直径的圆经过坐标原点
为直径的圆经过坐标原点 .
.
(1)求椭圆
 的标准方程;
的标准方程;(2)试探讨
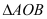 的面积
的面积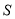 是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
是否为定值?若为定值,求出该定值;若不为定值,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在等腰梯形
 中,
中, ,
, 为
为 中点, 点
中点, 点 分别为
分别为 的中点, 将
的中点, 将 沿
沿 折起到
折起到 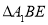 的位置,使得平面
的位置,使得平面 平面
平面 (如图
(如图 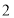 ).
).

(1)求证:
 ;
;(2)求直线
 与平面
与平面 所成角的正弦值;
所成角的正弦值;(3)侧棱
 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
 中,底面
中,底面 为菱形,侧面
为菱形,侧面 为等边三角形,且侧面
为等边三角形,且侧面 底面
底面 ,
,  ,
,  分别为
分别为 ,
,  的中点.
的中点.(Ⅰ)求证:
 .
.(Ⅱ)求证:平面
 平面
平面 .
.(Ⅲ)侧棱
 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关试题

