【题目】在△ABC中,角A,B,C所对边分别为a,b,c且acosC,bcosB,ccosA成等差数列.
(1)求B的值;
(2)求2sin2A﹣1+cos(A﹣C)的取值范围.
参考答案:
【答案】
(1)解:∵acosC,bcosB,ccosA成等差数列,∴2bcosB=acosC+ccosA,
由正弦定理可得:2sinBcosB=sinAcosC+sinCcosA=sin(A+C)=sinB,∵B∈(0,π),sinB≠0,
∴cosB= ![]() ,B=
,B= ![]()
(2)解:∵ ![]() ,∴A﹣C=2A﹣
,∴A﹣C=2A﹣ ![]() ,
,
∴ ![]()
= ![]() ,
,
∵ ![]() ,∴
,∴ ![]() <π,
<π,
∴- ![]() <
< ![]() ≤1,
≤1,
∴2sin2A﹣1+cos(A﹣C)的取值范 ![]()
【解析】(1)由于acosC,bcosB,ccosA成等差数列,可得2bcosB=acosC+ccosA,再利用正弦定理、和差化积、诱导公式等即可得出.(2)由 ![]() ,可得A﹣C=2A﹣
,可得A﹣C=2A﹣ ![]() ,再利用倍角公式即可化为2sin2A﹣1+cos(A﹣C)=
,再利用倍角公式即可化为2sin2A﹣1+cos(A﹣C)= ![]()
![]() ,由于
,由于 ![]() ,可得
,可得 ![]() <π,即可得出.
<π,即可得出.
【考点精析】根据题目的已知条件,利用正弦定理的定义和余弦定理的定义的相关知识可以得到问题的答案,需要掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
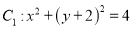 与圆
与圆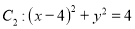
(1)若直线
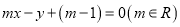 与圆
与圆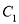 相交于
相交于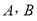 两个不同点,求
两个不同点,求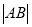 的最小值;
的最小值;(2)直线
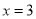 上是否存在点
上是否存在点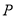 ,满足经过点
,满足经过点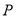 有无数对互相垂直的直线
有无数对互相垂直的直线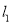 和
和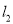 ,它们分别与圆
,它们分别与圆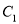 和圆
和圆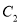 相交,并且直线
相交,并且直线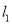 被圆
被圆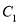 所截得的弦长等于直线
所截得的弦长等于直线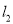 被圆
被圆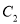 所截得的弦长?若存在,求出点
所截得的弦长?若存在,求出点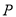 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是等差数列,满足a1=3,a5=15,数列{bn}满足b1=4,b4=20,且{bn﹣an}(n∈N+)是等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份
1
2
3
利润
2
3.9
5.5
(1)求利润
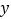 关于月份
关于月份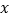 的线性回归方程;
的线性回归方程;(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式:
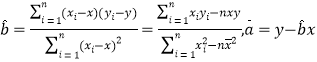 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】有三支股票
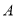 ,
,  ,
,  ,28位股民的持有情况如下:每位股民至少持有其中一支股票,在不持有
,28位股民的持有情况如下:每位股民至少持有其中一支股票,在不持有 股票的人中,持有
股票的人中,持有 股票的人数是持有
股票的人数是持有 股票的人数的2倍.在持有
股票的人数的2倍.在持有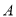 股票的人中,只持有
股票的人中,只持有 股票的人数比除了持有
股票的人数比除了持有 股票外,同时还持有其它股票的人数多1.在只持有一支股票的人中,有一半持有
股票外,同时还持有其它股票的人数多1.在只持有一支股票的人中,有一半持有 股票.则只持有
股票.则只持有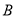 股票的股民人数是( )
股票的股民人数是( )A.
 B.
B. 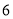 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
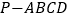 中,
中,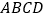 是边长为
是边长为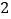 的棱形,且
的棱形,且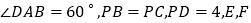 分别是
分别是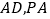 的中点.
的中点.(1)证明:
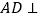 平面
平面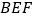 ;
;(2)若二面角
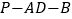 的大小为
的大小为 ,求点
,求点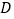 到平面
到平面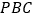 的距离.
的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
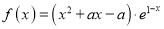 ,其中
,其中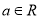 .
.(Ⅰ)求函数
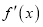 的零点个数;
的零点个数;(Ⅱ)证明:
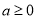 是函数
是函数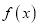 存在最小值的充分而不必要条件.
存在最小值的充分而不必要条件.
相关试题

