【题目】已知函数f(x)=ax﹣lnx﹣1,若曲线y=f(x)在点(2,f(2))处的切线与直线2x+y﹣1=0垂直.
(1)求a的值;
(2)函数g(x)=f(x)﹣m(x﹣1)(m∈R)恰有两个零点x1 , x2(x1<x2),求函数g(x)的单调区间及实数m的取值范围.
参考答案:
【答案】
(1)解:函数f(x)的定义域为(0,+∞)
由 ![]() ,且
,且 ![]() ,解得a=1.
,解得a=1.
(2)解:因为g(x)=(1﹣m)(x﹣1)﹣lnx,x∈(0,+∞)
则 ![]() .
.
(ⅰ)当1﹣m≤0即m≥1时,g'(x)<0,所以g(x)在(0,+∞)上单调递减
此时只存在一个零点,不合题意.
(ⅱ)当m<1时,令g'(x)=0,解得 ![]() .
.
当x变化时,g(x)与g'(x)的变化情况如下表:
x | (0, |
|
|
g'(x) | ﹣ | 0 | + |
g(x) | ↘ | 极小值 | ↗ |
由题意可知, ![]() .
.
下面判断极小值的正负.
设h(m)=m+ln(1﹣m),m<1
①当m=0时,h(0)=0,即g(x)极小=0
此时g(x)恰有一个零点不合题意
②当m≠0且m<1时, ![]()
当m<0时,h'(m)>0; 当0<m<1时,h'(x)<0
所以h(m)在(﹣∞,0)上单调递增,在(0,1)单调递减.
所以h(m)<h(0)=0,此时g(x)恰有两个零点.
综上,m的取值范围是(﹣∞,0)∪(0,1).
【解析】(1)求出f(x)的导数,根据 ![]() ,求出a的值即可;(2)求出g(x)的导数,通过讨论m的范围结合g(x)的单调性,求出g(x)的极小值,结合极小值的正负,求出m的范围即可.
,求出a的值即可;(2)求出g(x)的导数,通过讨论m的范围结合g(x)的单调性,求出g(x)的极小值,结合极小值的正负,求出m的范围即可.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】五一节期间,某商场为吸引顾客消费推出一项优惠活动,活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置,指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见表.
例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.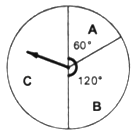
(1)已知顾客甲消费后获得n次转动转盘的机会,已知他每转一次转盘指针落在区域边界的概率为p,每次转动转盘的结果相互独立,设ξ为顾客甲转动转盘指针落在区域边界的次数,ξ的数学期望Eξ=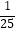 ,方差Dξ=
,方差Dξ= 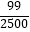 ,求n、p的值;
,求n、p的值;
(2)顾客乙消费280元,并按规则参与了活动,他获得返券的金额记为η(元).求随机变量η的分布列和数学期望.指针位置
A区域
B区域
C区域
返券金额(单位:元)
60
30
0
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=2x2+bx+c在
 上是减函数,在
上是减函数,在 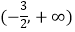 上是增函数,且两个零点x1 , x2满足|x1﹣x2|=2,求二次函数的解析式.
上是增函数,且两个零点x1 , x2满足|x1﹣x2|=2,求二次函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地建一座桥,两端的桥墩已建好,这两墩相距m米,余下的工程只需要建两端桥墩之间的桥面和桥墩.经预测一个桥墩的工程费用为256万元,距离为x米的相邻两墩之间的桥面工程费用为(2+
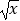 )x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.假设需要新建n个桥墩.
)x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.假设需要新建n个桥墩.
(1)写出n关于x的函数关系式;
(2)写出y关于x的函数关系式;
(3)当m=640米时,需新建多少个桥墩才能使y最小? -
科目: 来源: 题型:
查看答案和解析>>【题目】以下四个命题正确的个数( )
①用反证法证明数学命题时首先应该做出与命题结论相矛盾的假设.否定“自然数a,b,c中恰有一个奇数”时正确的反设为“自然数a,b,c中至少有两个奇数或都是偶数”;
②在复平面内,表示两个共轭复数的点关于实轴对称;
③在回归直线方程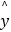 =﹣0.3x+10中,当变量x每增加一个单位时,变量
=﹣0.3x+10中,当变量x每增加一个单位时,变量 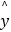 平均增加0.3个单位;
平均增加0.3个单位;
④抛物线y=x2过点( ,2)的切线方程为2x﹣y﹣1=0.
,2)的切线方程为2x﹣y﹣1=0.
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
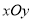 中,抛物线
中,抛物线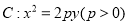 的焦点为
的焦点为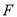 ,过点
,过点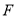 的直线
的直线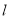 交
交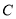 于
于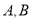 两点,交
两点,交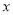 轴于点
轴于点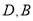 到
到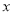 轴的距离比
轴的距离比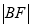 小
小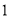 .
.(Ⅰ)求
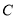 的方程;
的方程;(Ⅱ)若
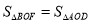 ,求
,求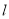 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男
女
合 计
爱好
40
20
60
不爱好
20
30
50
合 计
60
50
110
根据上述数据能得出的结论是( )
(参考公式与数据:X2= .当X2>3.841时,有95%的把握说事件A与B有关;当X2>6.635时,有99%的把握说事件A与B有关; 当X2<3.841时认为事件A与B无关.)
.当X2>3.841时,有95%的把握说事件A与B有关;当X2>6.635时,有99%的把握说事件A与B有关; 当X2<3.841时认为事件A与B无关.)
A.有99%的把握认为“爱好该项运动与性别有关”
B.有99%的把握认为“爱好该项运动与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”.
相关试题

