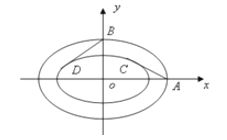
【题目】某奥运会主体育场的简化钢结构俯视图如图所示,内外两圈的钢骨架是离心率相同的椭圆,我们称这两个椭圆相似。
(1)已知椭圆![]() ,写出与椭圆
,写出与椭圆![]() 相似且焦点在
相似且焦点在![]() 轴上、短半轴长为
轴上、短半轴长为![]() 的椭圆
的椭圆![]() 的标准方程;若在椭圆
的标准方程;若在椭圆![]() 上存在两点
上存在两点![]() 、
、![]() 关于直线
关于直线![]() 对称,求实数
对称,求实数![]() 的取值范围;
的取值范围;
(2)从外层椭圆顶点A、B向内层椭圆引切线AC、BD,设内层椭圆方程为![]() +
+![]() =1 (a
=1 (a![]() b
b![]() 0),AC与BD的斜率之积为-
0),AC与BD的斜率之积为-![]() ,求椭圆的离心率。
,求椭圆的离心率。
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:
(1)由两点![]() 、
、![]() 关于直线
关于直线![]() 对称可设出直线
对称可设出直线![]() 的方程为
的方程为![]() ,将此方程与椭圆方程联立消去y可得
,将此方程与椭圆方程联立消去y可得![]() ,由题意此方程有两个不等实根,再根据
,由题意此方程有两个不等实根,再根据![]() 的中点在直线
的中点在直线![]() 上可消去t,根据判别式可得
上可消去t,根据判别式可得![]() 的范围;
的范围;
(2)设外层的椭圆的方程为![]() ,切线
,切线![]() 的方程为
的方程为![]() ,由直线与椭圆相切根据判别式为零可得
,由直线与椭圆相切根据判别式为零可得![]() ,同理切线BD的斜率
,同理切线BD的斜率![]() ,故
,故![]() ,结合条件可得
,结合条件可得![]() ,根据此结论可求得
,根据此结论可求得![]() 。
。
试题解析:
(1)椭圆![]() 的方程为:
的方程为: ![]()
设直线![]() 的方程为
的方程为![]() ,
,
由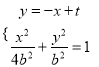 消去y整理得
消去y整理得![]()
设点![]() ,
, ![]() 中点为
中点为![]() ,
,
则![]()
所以![]()
因为中点![]() 在直线
在直线![]() 上,
上,
所以![]() ,
,
解得![]()
所以直线![]() 的方程为
的方程为![]() ,
,
由题意可知,直线![]() 与椭圆
与椭圆![]() 有两个不同的交点,
有两个不同的交点,
即方程![]() 有两个不同的实数解,
有两个不同的实数解,
所以![]() ,
,
解得![]() 或
或![]() (舍去)。
(舍去)。
所以实数![]() 的取值范围为
的取值范围为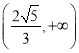 。
。
(2)设外层的椭圆的方程为![]() ,
,
设切线![]() 的方程为
的方程为![]() ,
,
由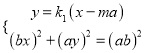 消去y整理得
消去y整理得
![]()
∵直线![]() 与椭圆相切,
与椭圆相切,
∴![]() ,
,
整理得![]() ,
,
同理![]()
∴![]() ,∴
,∴![]() ,
,
由题意得![]()
∴![]() ,∴
,∴![]() 。
。
即椭圆的离心率为![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】过椭圆
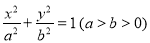 的左顶点
的左顶点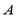 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为 ,与
,与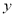 轴的交点为
轴的交点为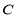 ,已知
,已知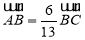 .
.(1)求椭圆的离心率;
(2)设动直线
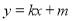 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点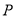 ,且与直线
,且与直线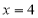 相交于点
相交于点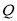 ,若
,若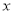 轴上存在一定点
轴上存在一定点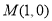 ,使得
,使得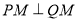 ,求椭圆的方程.
,求椭圆的方程. -
科目: 来源: 题型:
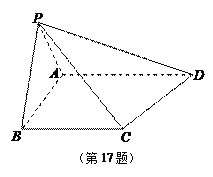
查看答案和解析>>【题目】如图,在四棱锥
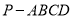 中,平面
中,平面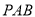
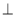 平面
平面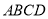 ,BC//平面PAD,
,BC//平面PAD, 
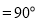 ,
,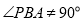 .
.
求证:(1)
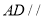 平面
平面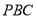 ;
;(2)平面
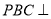 平面
平面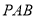 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
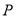 是菱形
是菱形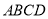 所在平面外一点,
所在平面外一点, 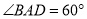 ,
, 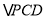 是等边三角形,
是等边三角形, 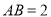 ,
, 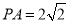 ,
, 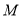 是
是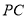 的中点.
的中点.(Ⅰ)求证:
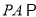 平面
平面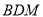 ;
;(Ⅱ)求证:平面
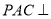 平面
平面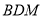 ;
;(Ⅲ)求直线
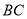 与平面
与平面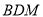 的所成角的大小.
的所成角的大小.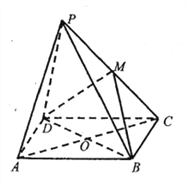
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,命题
,命题 椭圆C1:
椭圆C1:  表示的是焦点在
表示的是焦点在 轴上的椭圆,命题
轴上的椭圆,命题 对
对 ,直线
,直线 与椭圆C2:
与椭圆C2:  恒有公共点.
恒有公共点.(1)若命题“
 ”是假命题,命题“
”是假命题,命题“ ”是真命题,求实数
”是真命题,求实数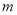 的取值范围.
的取值范围.(2)若
 真
真 假时,求椭圆C1、椭圆C2的上焦点之间的距离d的范围。
假时,求椭圆C1、椭圆C2的上焦点之间的距离d的范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
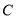 :
: 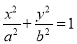 (
(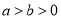 )与
)与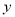 轴交于
轴交于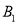 ,
, 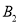 两点,
两点, 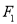 为椭圆
为椭圆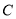 的左焦点,且
的左焦点,且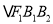 是边长为2的等边三角形.
是边长为2的等边三角形.(Ⅰ)求椭圆
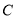 的方程;
的方程;(Ⅱ)设直线
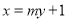 与椭圆
与椭圆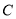 交于
交于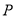 ,
, 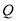 两点,点
两点,点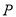 关于
关于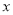 轴的对称点为
轴的对称点为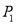 (
(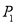 与
与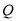 不重合),则直线
不重合),则直线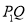 与
与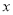 轴交于点
轴交于点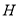 ,求
,求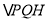 面积的取值范围.
面积的取值范围. -
科目: 来源: 题型:
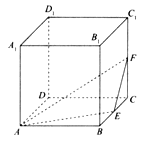
查看答案和解析>>【题目】(文科选做)如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E、F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面AEF,则线段A1P长度的取值范围是_____。
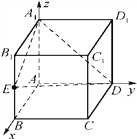
(理科选做)在正方体ABCD-A1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD所成的锐二面角的余弦值为________.
相关试题

