【题目】如图,在四棱锥![]() 中,平面
中,平面![]()
![]() 平面
平面![]() ,BC//平面PAD,
,BC//平面PAD, ![]()
![]() ,
,![]() .
.
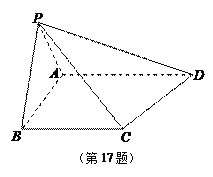
求证:(1) ![]() 平面
平面![]() ;
;
(2)平面![]() 平面
平面![]() .
.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)由BC//平面PAD可得BC//AD,根据线面平行的判定定理可得![]() 平面
平面![]() ;(2)过P作PH
;(2)过P作PH ![]() AB于H,由条件可得
AB于H,由条件可得![]() 平面
平面![]() ,从而可证得BC
,从而可证得BC ![]() PH,又BC
PH,又BC ![]() PB,故有BC
PB,故有BC ![]() 平面PAB,所以平面PBC
平面PAB,所以平面PBC ![]() 平面PAB .
平面PAB .
试题解析:
(1)因为BC//平面PAD,
而BC![]() 平面ABCD,平面ABCD
平面ABCD,平面ABCD![]() 平面PAD = AD,
平面PAD = AD,
所以BC//AD ,
又因为AD ![]() 平面PBC,BC
平面PBC,BC![]() 平面PBC,
平面PBC,
所以![]() 平面
平面![]()

(2)过P作PH ![]() AB于H,
AB于H,
因为平面![]()
![]() 平面
平面![]() ,且平面
,且平面![]()
![]() 平面
平面![]() =AB,
=AB,
所以![]() 平面
平面![]()
因为BC ![]() 平面ABCD,
平面ABCD,
所以BC ![]() PH.
PH.
因为![]()
![]() ,
,
所以BC ![]() PB,
PB,
而![]() ,
,
于是点H与B不重合,即PB ![]() PH = H.
PH = H.
因为PB,PH ![]() 平面PAB,
平面PAB,
所以BC ![]() 平面PAB
平面PAB
因为BC ![]() 平面PBC,
平面PBC,
故平面PBC ![]() 平面
平面![]() AB.
AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求下列函数的定义域
(1)f(x)= ;
;
(2)f(x)=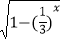 ;
;
(3)f(x)=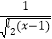 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
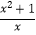 (x≠0).
(x≠0).
(1)证明函数f(x)为奇函数;
(2)判断函数f(x)在[1,+∞)上的单调性,并说明理由;
(3)若x∈[﹣2,﹣3],求函数的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】过椭圆
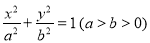 的左顶点
的左顶点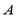 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为 ,与
,与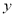 轴的交点为
轴的交点为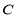 ,已知
,已知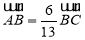 .
.(1)求椭圆的离心率;
(2)设动直线
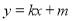 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点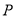 ,且与直线
,且与直线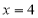 相交于点
相交于点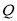 ,若
,若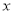 轴上存在一定点
轴上存在一定点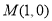 ,使得
,使得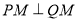 ,求椭圆的方程.
,求椭圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
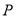 是菱形
是菱形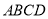 所在平面外一点,
所在平面外一点, 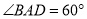 ,
, 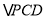 是等边三角形,
是等边三角形, 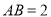 ,
, 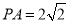 ,
, 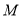 是
是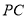 的中点.
的中点.(Ⅰ)求证:
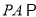 平面
平面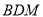 ;
;(Ⅱ)求证:平面
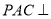 平面
平面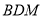 ;
;(Ⅲ)求直线
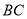 与平面
与平面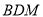 的所成角的大小.
的所成角的大小.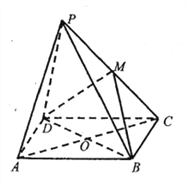
-
科目: 来源: 题型:
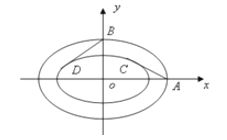
查看答案和解析>>【题目】某奥运会主体育场的简化钢结构俯视图如图所示,内外两圈的钢骨架是离心率相同的椭圆,我们称这两个椭圆相似。
(1)已知椭圆
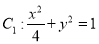 ,写出与椭圆
,写出与椭圆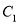 相似且焦点在
相似且焦点在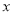 轴上、短半轴长为
轴上、短半轴长为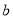 的椭圆
的椭圆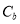 的标准方程;若在椭圆
的标准方程;若在椭圆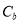 上存在两点
上存在两点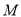 、
、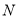 关于直线
关于直线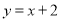 对称,求实数
对称,求实数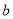 的取值范围;
的取值范围;(2)从外层椭圆顶点A、B向内层椭圆引切线AC、BD,设内层椭圆方程为
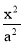 +
+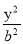 =1 (a
=1 (a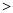 b
b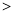 0),AC与BD的斜率之积为-
0),AC与BD的斜率之积为-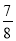 ,求椭圆的离心率。
,求椭圆的离心率。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,命题
,命题 椭圆C1:
椭圆C1:  表示的是焦点在
表示的是焦点在 轴上的椭圆,命题
轴上的椭圆,命题 对
对 ,直线
,直线 与椭圆C2:
与椭圆C2:  恒有公共点.
恒有公共点.(1)若命题“
 ”是假命题,命题“
”是假命题,命题“ ”是真命题,求实数
”是真命题,求实数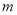 的取值范围.
的取值范围.(2)若
 真
真 假时,求椭圆C1、椭圆C2的上焦点之间的距离d的范围。
假时,求椭圆C1、椭圆C2的上焦点之间的距离d的范围。
相关试题

