【题目】如图,在四棱锥 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是
是 ![]() 的中点,
的中点, ![]() 是棱
是棱 ![]() 上的点,
上的点, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)求证:平面 ![]() 底面
底面 ![]() ;
;
(2)设 ![]() ,若二面角
,若二面角 ![]() 的平面角的大小为
的平面角的大小为 ![]() ,试确定
,试确定 ![]() 的值.
的值.
参考答案:
【答案】
(1)
证明:∵AD//BC,BC= ![]() ,Q是AD的中点,
,Q是AD的中点,
∴BC ![]() DQ,则四边形BCDQ为平行四边形,从而CD//BQ.
DQ,则四边形BCDQ为平行四边形,从而CD//BQ.
∵AD⊥CD,∴QB⊥AD.
∵PA=PD=2,AD=2,Q是AD的中点,∴ ![]()
又∵QB=CD= ![]() ,
, ![]()
∴ ![]() ,即PQ⊥QB,又PQ
,即PQ⊥QB,又PQ ![]() AD=Q,∴BQ⊥平面PAD,∴平面PAD⊥底面ABCD.
AD=Q,∴BQ⊥平面PAD,∴平面PAD⊥底面ABCD.
(2)
解:∵PA=PD=2,Q是AD的中点,∴PQ⊥AD.∵平面PAD⊥平面ABCD,且平面PAD ![]() 平面ABCD=AD,∴PQ⊥平面ABCD.如图,以Q为原点建空间直角坐标系.
平面ABCD=AD,∴PQ⊥平面ABCD.如图,以Q为原点建空间直角坐标系.
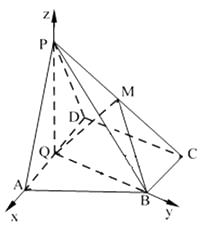
则平面BQC的法向量为 ![]()
设 ![]() ,则
,则 ![]() ,∵
,∵ ![]() ,∴
,∴ ![]()
则 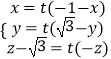 ,即
,即 ![]() ,
, ![]() ,
, ![]() ,在平面MBQ中,
,在平面MBQ中, ![]() ,
, ![]() ,设平面MBQ的法向量为
,设平面MBQ的法向量为 ![]() ,由
,由 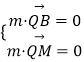 ,得
,得 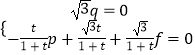 ,取f=t,得
,取f=t,得 ![]() .∴平面MBQ的一个法向量为
.∴平面MBQ的一个法向量为 ![]()
∵二面角M-BQ-C的平面角的大小为30°,∴ 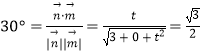 ,解得t=3.
,解得t=3.
【解析】本题主要考查空间直线与平面垂直、平面与平面垂直、直线与直线垂直的判定与性质,二面角等基础知识,考查空间想象能力,推理论证能力,运算求解能力,以及数形结合思想、化归与转化思想.
【考点精析】通过灵活运用直线与平面垂直的判定和平面与平面垂直的判定,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;一个平面过另一个平面的垂线,则这两个平面垂直即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 ,则下列结论错误的是( )
,则下列结论错误的是( )A.
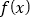 是偶函数 B.
是偶函数 B. 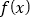 的值域是
的值域是
C. 方程
 的解只有
的解只有 D. 方程
D. 方程 的解只有
的解只有
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 在
在 和
和 处取得极值.
处取得极值.(1)求f(x)的表达式和极值.
(2)若f(x)在区间[m,m+4]上是单调函数,试求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量(百件)与销售单价x(元/件)之间的关系用下图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.

(1)把y表示为x的函数;
(2)当销售价为每件50元时,该店正好收支平衡(即利润为零),求该店的职工人数;
(3)若该店只有20名职工,问销售单价定为多少元时,该专卖店可获得最大月利润?(注:利润=收入-支出)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“中国人均读书4.3本(包括网络文学和教科书),比韩国的11本、法国的20本、日本的40本、犹太人的64本少得多,是世界上人均读书最少的国家.”这个论断被各种媒体反复引用.出现这样的统计结果无疑是令人尴尬的,而且和其他国家相比,我国国民的阅读量如此之低,也和我国是传统的文明古国、礼仪之邦的地位不相符.某小区为了提高小区内人员的读书兴趣,特举办读书活动,准备进一定量的书籍丰富小区图书站,由于不同年龄段需看不同类型的书籍,为了合理配备资源,现对小区内看书人员进行年龄调查,随机抽取了一天
 名读书者进行调查,将他们的年龄分成6段:
名读书者进行调查,将他们的年龄分成6段:  ,
,  ,
,  ,
,  ,
,  ,
,  后得到如图所示的频率分布直方图.问:
后得到如图所示的频率分布直方图.问:
(1)估计在40名读书者中年龄分布在 的人数;
的人数;
(2)求40名读书者年龄的平均数和中位数;
(3)若从年龄在 的读书者中任取2名,求这两名读书者年龄在
的读书者中任取2名,求这两名读书者年龄在  的人数
的人数  的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设椭圆的中心为原点
 ,长轴在
,长轴在 轴上,上顶点为
轴上,上顶点为 ,左,右焦点分别为
,左,右焦点分别为 ,线段
,线段 的中点分别为
的中点分别为 ,且
,且 是面积为4的直角三角形.
是面积为4的直角三角形.(1)求该椭圆的离心率和标准方程;
(2)过
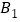 做直线
做直线 交椭圆于
交椭圆于 两点,使
两点,使 ,求直线
,求直线 的方程.
的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知

(1)设
 ,
, ,若函数
,若函数 存在零点,求a的取值范围;
存在零点,求a的取值范围;(2)若
 是偶函数,求
是偶函数,求 的值;
的值;(3)在(2)条件下,设
 ,若函数
,若函数 与
与 的图象只有一个公共点,求实数b的取值范围.
的图象只有一个公共点,求实数b的取值范围.
相关试题

